|
Question 1162067: In this investigation, you will be estimating the values of √40 √75 √90 √245 √450 √640 √675 and to the nearest hundredths place.
1. Describe clearly what strategy you plan to use to estimate these values.
2. Estimate the values to the nearest hundredth and show or briefly describe your work.
Radical
Work
Estimation
3. Reflect on the calculations you made. What general methods or short cuts did you find to make the calculations easier as you did each calculation?
Found 4 solutions by Alan3354, josgarithmetic, ikleyn, greenestamps:
Answer by Alan3354(69443)   (Show Source):
Answer by josgarithmetic(39623)  (Show Source):
Answer by ikleyn(52832)  (Show Source):
You can put this solution on YOUR website! .
In this investigation, you will be estimating the values of √40 √75 √90 √245 √450 √640 √675 and to the nearest hundredths place.
1. Describe clearly what strategy you plan to use to estimate these values.
2. Estimate the values to the nearest hundredth and show or briefly describe your work.
Radical
Work
Estimation
~~~~~~~~~~~~~~~~~~~~~~
After reading your post, I have a QUESTION.
Do you ask to estimate each and every square root separately (as you use the term "values" in the post),
or the entire product as one single number (as it is actually written in the post) ?
Do you see, the right strategy of solving problem STARTS from understanding what is written in its condition.
And it is YOURS DIRECT/straight DUTY to bring the condition in the correct and clear form.
But from your writing, I clearly see that you do not understand at all what you write in the post,
and even do not care about it.
Which is VERY SAD . . .
-------------
With such skills, there is nothing to do for you at this forum.
Learn to be responsible with your writing and learn on how to write Math problems correctly and accurately.
Have a nice day (!)
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
It's impossible for us to know what YOU are expected to do with this; so we can only show you what WE would do.
The concept of estimating a square root to the nearest hundredth is a bit strange. There is an algorithm for finding a square root by hand which is not too difficult to use; it can be used to find the square root to as many decimal places as you want.
Finding a square root by performing calculations instead of using the algorithm would be extremely awkward, so you would probably want to use some tool like a calculator to help. But if you have a calculator, you can find the square root directly.
So again I'm not sure what you are being asked to do here.
But I will show you a relatively quick way to find the square roots.
Here is the strategy we will use:
(1) Start with a guess. It doesn't even have to be a reasonable guess; but you will get to the desired result faster if it is.
(2) Divide the given number by the guess. If the guess was too small, the number divided by the guess will be too large, and vice versa. So the average of the guess and the number divided by the guess will be closer to the actual square root. So
(3) Find the average of the guess and the number divided by the guess.
(4) Repeat steps 2 and 3 until the desired precision is achieved.
Formally, if the given number is n and  is the original guess, then subsequent guesses  will be computed as
This recursive formula is easy to use on a good scientific calculator, or in an Excel spreadsheet.
Here is the calculation for the first example,  .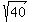
 [the square root of 40 is between 6 and 7]
 = 6.33333...
 = 6.32456...
That is already accurate to 5 decimal places....
I'll show one more, in which I will use an initial guess that is not very good, to show that the process will still converge quickly.
For 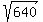 , with an initial guess of 10....
 = 37
 = 27.14865...
 = 25.36128...
 = 25.29830...
 = 25.29822128...
That answer is correct to 8 decimal places
I have no idea whether that is anything like what you were looking for.
Note that all of the given square roots can be simplified in radical form:
...
And so on.
But the process described above converges so quickly that simplifying the square roots in radical form is essentially a waste of time.
On the other hand, I suspect simplifying the square roots in radical form MIGHT have been one of the things you were EXPECTED to do in this assignment....
So again, for the n-th time, I don't know what YOU were expected to do with this assignment.
|
|
|
| |
