Question 1046622: I am stuck on Guass's Approach with odd numbers. The problem is 1+3+5+7+...+999. I've looks for examples everywhere. I hope you can help!
Found 2 solutions by ikleyn, Theo:
Answer by ikleyn(52781)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! gauss's trick is described here.
https://nzmaths.co.nz/gauss-trick-staff-seminar
i used his method to determine the value of the sum of the odd number from 1 to 999.
the sum of the number from 1 to 1000 can be found as follows:
in normal order, the sequence is 1,2,3,4,5.
in reverse order, the sequence is 1000,999,998,997,994
pair the normal order terms with the reverse order terms and you get:
1 + 1000 = 1001
2 + 999 = 1001
3 + 998 = 1001
etc.
there are 1000 of such pairings.
1000 * 1001 = 1001000.
that's double the sum of 1 to 1000.
divide that by 2 and you get the sum of the numbers from 1 to 1000 = 500500.
there are 500 pairs of numbers from 1 to 1000.
the pairs are:
1,2
3,4
5,6
etc.
in each pair, the even number is 1 more than the odd number.
since there are 500 pairs, then the sum of the even numbers will be 500 more than the sum of the odd numbers.
let x = the sum of the odd number.
x + 500 is the sum of the even numbers.
you get x + x + 500 = 500500
simplify to get 2x + 500 = 500500
subtract 500 from 500500 to get:
2x = 500000
divide both sides by 2 to get:
x = 250000
that's the sum of the odd numbers.
the sum of the even numbers is 250500
add them up and you get the sum of the number is 500500.
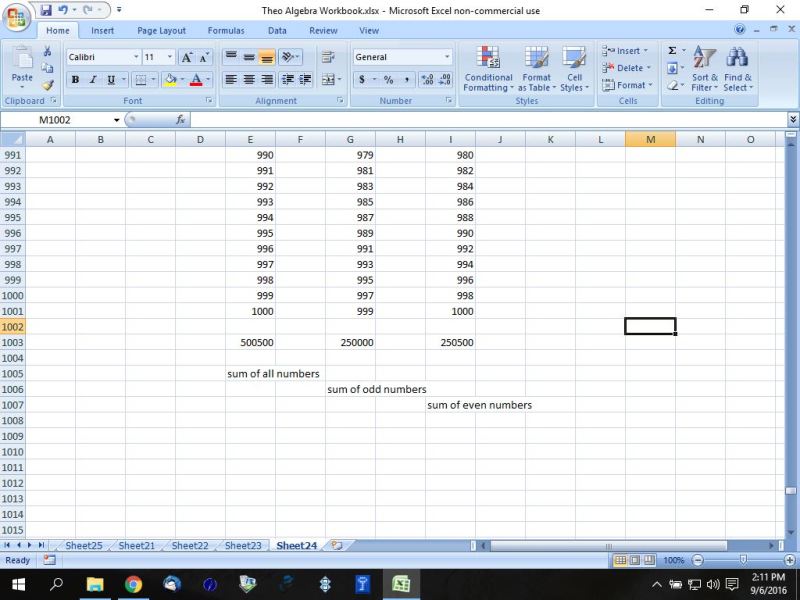
i check with excel and got those tallies, so the formula works.
the sum of the odd number is 250,000.
the sum of the even numbers is 250,500.
here's a picture of my excel analysis.
|
|
|