Question 981006: If S1,S2,S3 be the sum of n,2n,3n terms respectively of an A.P.Then (a)S3=S1+S2
(b)S3=2(S1+S2) (c)S3=3(S2-S1) (d)S3=3(S1+S2)
If Sn denotes the sum of first n terms of an A.P and S2n=3Sn,then S3n/Sn=
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If 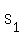 , , 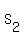 , and , and 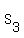 are the sums of are the sums of  , ,  , ,  terms respectively of an A.P., then terms respectively of an A.P., then  . .
ONE WAY TO SOLVE THE PROBLEM is to applying somewhat involved algebraic manipulations,
and (possibly memorized) formulas derived from (possibly forgotten, possibly never fully understood) concepts:
For an A.P. with first term  and common difference and common difference  , ,
Sum of first  terms = terms =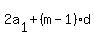 <---> <---> 
For  , we have , we have  . .
For  , we have , we have  . .
For  , we have , we have  . .
 , ,
so the three choices with 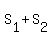 do not work. do not work.
On the other hand,
 , ,
so 
ANOTHER WAY TO LOOK AT THE PROBLEM
involves visualizing what those sums are made of and how they are related,
relying more on concepts than on formulas,
and using easier arithmetic rather than advanced algebra.
Unfortunately, describing a clear reasoning based on basic concepts often takes a lot of words (or a lot of algebraic expressions).
Let the terms of the A.P. be  , ,  , ,  , etc. , etc.



We know that each term is the one before plus  , ,
and the difference between two terms is  times the difference between the term numbers, times the difference between the term numbers,
as in  <---> <---> 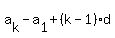 , ,
so  , ,
but that applies more generally, not just when one of those two terms is  , ,
so  , ,  , and so on up to , and so on up to
 . .
So,  . .
We can write 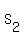 as a function of as a function of  and and  : :
 <--> <-->  . .
By a similar reasoning,
since  , ,  , and so on, up to , and so on, up to  , ,
 , ,
so  , ,
and  ---> --->  . .
We can write 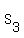 as a function of as a function of  and and  : :
 <--> <-->  . .
Looking at  , ,
it is clear that none of the formulas with  will work, will work,
but  ---> --->
NOW FOR THE EASY PROBLEM:
If 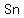 denotes the sum of first denotes the sum of first  terms of an A.P., terms of an A.P.,
and  , then , then  = ? = ?
We proved above that if 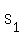 , , 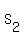 , and , and 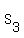 are the sums of are the sums of  , ,  , ,  terms respectively of an A.P., then terms respectively of an A.P., then  . .
Using the easier symbols from the problem above,
the new question is
if  , then , then 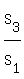 = ? = ?
 , so , so
 ---> ---> ---> --->
|
|
|