SOLUTION: If the first two terms of a geometric sequence are 2 and 1, respectively, which term of the sequence is equal to 1/16?

Algebra ->  Sequences-and-series -> SOLUTION: If the first two terms of a geometric sequence are 2 and 1, respectively, which term of the sequence is equal to 1/16?      Log On


   

Question 979019: If the first two terms of a geometric sequence are 2 and 1, respectively, which term of the sequence is equal to 1/16?
Answer by MathLover1(20849) About Me  (Show Source):
You can put this solution on YOUR website!
In a Geometric Sequence each term is found by multiplying the previous term by a constant.
In general we write a Geometric Sequence like this:
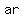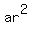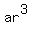{ a, ar, ar%5E2, ar%5E3, ... }
where:
a is the first term, and
r is the factor between the terms (called the "common ratio")
so, if first term is a=2 and second term is ar=1, a constant (the "common ratio") is r=1%2F2
and your sequence looks like this:
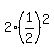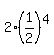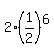{ 2, 1, 2%2A%281%2F2%29%5E2, 2%2A%281%2F2%29%5E3, 2%2A%281%2F2%29%5E4,2%2A%281%2F2%29%5E5,2%2A%281%2F2%29%5E6... }
so, we can find out which term is 1%2F16 using the rule
to calculate any term:
a%5Bn%5D+=+ar%5E%28n-1%29
(We use "n-1" because 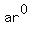ar%5E0 is for the 1st term)
a%5Bn%5D+=+1%2F16
ar%5E%28n-1%29=1%2F16
2%2A%281%2F2%29%5E%28n-1%29=1%2F16
%281%2F2%29%5E%28n-1%29=1%2F32
%281%2F2%29%5E%28n-1%29=1%2F2%5E5
%281%2F2%29%5E%28n-1%29=%281%2F2%29%5E5
n-1=5
n=5%2B1
=> n=6......so, it is 6th term
check:
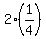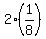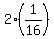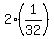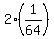{ 2, 1, 2%281%2F4%29, 2%2A%281%2F8%29, 2%2A%281%2F16%29,2%2A%281%2F32%29,2%2A%281%2F64%29,... }
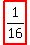{ 2, 1, 1%2F2, 1%2F4, 1%2F8,highlight%281%2F16%29,1%2F32,... }