SOLUTION: please help me find the sum of the following sequence (-6)+(-1)+4+9+...+39 thank you

Algebra ->  Sequences-and-series -> SOLUTION: please help me find the sum of the following sequence (-6)+(-1)+4+9+...+39 thank you      Log On


   

Question 929332: please help me find the sum of the following sequence (-6)+(-1)+4+9+...+39 thank you
Found 2 solutions by Fombitz, KMST:
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
First find the sequence.
a%5Bn%5D=-11%2B5n
Then find n for the last term.
39=-11%2B5n
50=5n
n=10
Then use the sum formula,
S%5Bn%5D=%28n%2F2%29%28a%5B1%5D%2Ba%5Bn%5D%29
S%5B10%5D=%2810%2F2%29%28-6%2B39%29
S%5B10%5D=5%2833%29
highlight%28S%5B10%5D=165%29

Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The sum (-6)+(-1)+4+9+...+39 is the sum of an arithmetic sequence
whose first term is 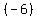%28-6%29 ,
and each term is equal to the term before plus the common difference: 5 .
For a timed test, I would solve the problem by mental math to save time.
If a pesky teacher insists on "show your work", I would go the formula-happy way.

THE MENTAL MATH WAY:
How many terms?
There are 10 terms.
There are 2 negative terms,
and the positive terms go from 4=5%2A1=1%2A5-1 to 39=40-1=8%2A5-1 ,
so without listing and counting, I know there are 8 positive terms.
So the total number of terms is 8%2B2=10 .
The sum is the average of the terms times the number of terms,
but in an arithmetic sequence,
the average of the terms is the same as the average of the first and last terms
(which is the sum of the first and last terms divided by 2 ).
That sum is %28-6%29%2B39=33 ,
and that sum times 10 and divided by 2 is 33%2A10%2F2=highlight%28165%29

THE FORMULA-HAPPY WAY:
First we make sure that it is an arithmetic sequence, meaning that there is a common difference, d , between consecutive terms:
%28-1%29-%28-6%29=5 ,
4-%28-1%29=5 , and
9-4=5 , so it is an arithmetic sequence,
and d=5 .
The first term is a%5B0%5D=-6 .
We know that, in an arithmetic sequence, term number n is
a%5Bn%5D=a%5B0%5D%2B%28n-1%29%2Ad ,
so we apply that formula to term 39 , to find what is its term number, n .
39=-6%2B%28n-1%29%2A5-->39%2B6=%28n-1%29%2A5-->45=%28n-1%29%2A5-->45%2F5=n-1-->9=n-1-->9%2B1=n-->n=10 .
Now we apply a formula to find
the sum s%5Bn%5D of the first n=10 terms of an arithmetic sequence with a[0]=-6}}} and d=5 .
With sum luck, we were given the formula
S%5Bn%5D=n%2A%28a%5B0%5D%2Ba%5Bn%5D%29%2F2 .
If so, we apply it and get
S%5B10%5D=10%2A%28%28-6%29%2B39%29%2F2=10%2A33%2F2=330%2F2=highlight%28165%29 .
Without luck, we may only have another more cumbersome formula, less convenient for this particular problem, like
S%5Bn%5D=n%2A%282%2Aa%5B0%5D%2B%28n-1%29%2Ad%29%2F2 ,
and we could apply that formula to get
.