SOLUTION: Three consecutive numbers of a G.p are such that there sum is 26 and there product is 216.Find the numbers

Algebra ->  Sequences-and-series -> SOLUTION: Three consecutive numbers of a G.p are such that there sum is 26 and there product is 216.Find the numbers      Log On


   

Question 858284: Three consecutive numbers of a G.p are such that there sum is 26 and there product is 216.Find the numbers
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
THE FAST WAY:
If the product is 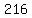216 ,
216=6%5E3=%282%2A3%29%5E3=2%5E3%2A3%5E2
The product of the three terms could be
2%2A%282%2A3%29%2A%282%2A3%5E2%29=216 with the terms being 2, 6, and 18 (or 18, 6, and 2)
or
the product could be
3%2A%283%2A2%29%2A%283%2A2%5E2%29=216 with the terms being 3, 6, and 12 (or 12, 6, and 3)

18%2B2%2B6=26 while 12%2B6%2B3=21 , so the numbers are
highlight%282%29 , highlight%286%29 , and highlight%2818%29 .
That gives as a solution quickly, without proving that it is the only solution.

THE EXPECTED WAY (with lots of formulas and calculations):
We will call the first term we are looking for b%5B1%5D=b ,
and the common ratio r .
The formula for term number n is b%5Bn%5D=b%5B1%5D%2Ar%5E%28n-1%29 .
The second and third terms would be
b%5B2%5D=b%2Ar and b%5B3%5D=b%2Ar%5E2 .
Their product would be b%2A%28b%2Ar%29%2A%28b%2Ar%5E2%29=b%5E3%2Ar%2A3=%28br%29%5E3
We could calculate their sum as
SUM=B%2Bbr%2Bbr%5E3=b%28r%5E2%2Br%2B1%29
Otherwise, the formula for the sum of the first n terms is
SUM%5Bn%5D=b%5B1%5D%28r%5En-1%29%2F%28r-1%29 .
The sum of the three terms would be
SUM=b%28r%5E3-1%29%2F%28r-1%29=%28br%5E3-b%29%2F%28r-1%29
Our equations are
b%5E3%2Ar%2A3=216 or %28br%29%5E3=216 and
b%28r%5E3-1%29%2F%28r-1%29=26%29 or %28br%5E3-b%29%2F%28r-1%29=26%29 or b%28r%5E2%2Br%2B1%29=26 .
From %28br%29%5E3=216 we get br=root%283%2C210%29-->br=6-->system%28b=6%2Fr%2C%22or%22%2Cr=6%2Fb%29
If we substitute either one into b%28r%5E2%2Br%2B1%29=26 we get an equation in one variable that we can solve.
%286%2Fr%29%28r%5E2%2Br%2B1%29=26-->6%28r%5E2%2Br%2B1%29=26r-->6r%5E2%2B6r%2B6=26r-->6r%5E2%2B6r%2B6-26r=0-->6r%5E2-20r%2B6=0<-->3r%5E2-10r%2B3=0
No matter how we solve 6r%5E2-20r%2B6=0 or 3r%5E2-10r%2B3=0
we find system%28r=3%2C%22or%22%2Cr=1%2F3%29 .
system%28r=3%2Cb=6%2Fr%29-->system%28r=3%2Cb=6%2F3%29-->highlight%28system%28r=3%2Cb=2%29%29--> the terms , in order, are 2, 6, and 18.
system%28r=1%2F3%2Cb=6%2Fr%29-->system%28r=3%2Cb=6%2F%281%2F3%29%29-->system%28r=1%2F3%2Cb=6%2A3%29-->highlight%28system%28r=1%2F3%2Cb=18%29%29--> the terms , in order, are 18, 6, and 2.
The terms (regardles of order are highlight%282%29 , highlight%286%29 , and highlight%2818%29 ,
and that is the only solution