Find the type of sequence. This is a geometric sequence with a common term of 1/4, because each term * 1/4 is the next term.
For any geometric sequence, the nth term =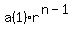 
where a(1) is the first term, n is the term number you're trying to find, and r is the common ratio.
Let's test it with the third term. The third term =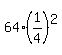 
= 64/16 = 4. That is the third term. See, it works!
The tenth term is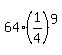 
= 64/262144 = 1/4096. The answer is c.
If you didn't remember the formula, write out the terms, dividing each subsequent term by 4 (which is multiplying it by 1/4), until you reach the 10th term.
64, 64/4=16, 16/4=4, 4/4=1, 1/4=1/4, 1/4 / 4 = 1/16, 1/16 / 4 = 1/64, 1/64 / 4 = 1/256, 1/256/4 = 1/1024, 1/1024 / 4 = 1/4096.
(