Question 1162188: In an arithmetic progression, the sum of the first ten terms is 50 and the 5th term is three times the second term. Find the A. First term. B. Common difference. C. The sum of the first 100 terms
Found 2 solutions by MathLover1, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
an arithmetic progression:
 , , 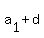 , ,  ,.... where ,.... where  is the first term and is the first term and  is Common difference is Common difference
nth term formula:

Denote this partial sum by  . Then . Then
 ,where ,where  is the number of terms, is the number of terms,  is the first term and is the first term and  is the last term is the last term
given: the sum of the first ten terms is 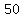
-> 



 .......solve for .......solve for 
 .... ....




 .....eq.1 .....eq.1
the 5th term is three times the second term:
 -> -> and and 



 ......... ..eq.2 ......... ..eq.2
substitute in eq1
 .....eq.1 .....eq.1





 -> First term -> First term
go to eq.2
 ......... ..eq.2 ......... ..eq.2

 ->Common difference ->Common difference
nth term formula:

first  terms are: terms are:
 , , 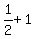 , , 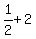 , , 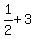 , ,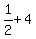 , ,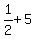 , , , , 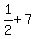 , ,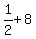 , ,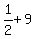
or
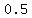 , ,  , ,  , ,  , , , ,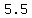 , , , ,  , ,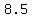 , ,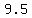
check their sum:


 -> true -> true
The sum of the first  terms: terms:
first find  th term: th term:
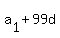 -> -> 
then the sum is:



Answer by MathTherapy(10552)   (Show Source): (Show Source):
|
|
|