Question 1125867: What is the next numbers in these sequences and why are they as they are:
-9 -8 -4 5 21 46 ... ...
and
2 4 6 10 16 26 42 ... ...
Thank you
Found 2 solutions by Boreal, MathLover1:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! The difference between the numbers in the first one ar 1,4,9,16,25, all perfect squares of 1-5. The next difference will be 6^2 or 36, so the number will be 46+36, or 82. After that, it will be 118, 200.
The first two numbers add to equal the third. Each number is the sum of the preceding two. So the next number in the series will be 26+42, or 68.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1.
 , ,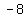 , ,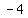 , , , , , ,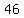 ... ... ... ...
Find nth term formula using differences.
Differences:
 | | | |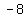 | | | |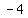 | | | |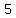 | | | |  | | | | 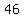
..... |  | | | | | | | |  | | | |  | | | |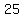 | |
............ | | 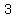 | | | | | | | | | | | |  | | | |
............. | | | | | | |  | | | | | |
since we have three differences, the general form for finding the nth term in a cubic sequence is

Set up a system of four equations with four variables to find the coefficients  , ,  , ,  and and  . .
Use the values given in the sequence as if they were points on a graph in the form ( , ,  ). ).
It is easiest to start with the first  terms, as they are usually smaller or simpler numbers to work with. terms, as they are usually smaller or simpler numbers to work with.
so, we have:
( , ,  ), ( ), ( , ,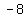 ), ( ), ( , , ), ( ), ( , , ) )
Plug in to:

( , ,  ) )

 ...............eq.1 ...............eq.1
( , ,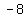 ) )

 ...............eq.2 ...............eq.2
( , , ) )

 ...............eq.3 ...............eq.3
( , , ) )

 ...............eq.4 ...............eq.4
Solve the system of  equations using your favorite method. equations using your favorite method.
In this example, the results are:
 , ,  , ,  , , 
then we have

and next term will be:



here are some more terms:
 , ,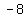 , ,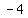 , , , , , ,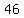 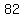 , , , , , ,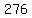 , , , , ............. .............
2.
 , ,  , ,  , ,  , , , , 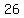 , ,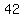 , ... . , ... .
track the sequence of  the previous the previous  numbers combined: numbers combined:





so, the next term will be:

your answer is: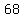
some more terms:
 , ,  , ,  , ,  , ,  , , 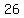 , ,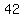 , , 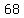 , , 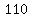 , ,  , ,  , ,  , , 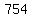 , , 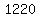 , ... , ...
|
|
|