Question 1100175: Fimd six numbers in AP, such that the sum of the two extremes be 16 and the product of the two middle terms be 63.
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the sum of the first and last numbers is an integer and the product of the two middle terms is an integer, then almost certainly all the numbers will be integers.
Then if the product of the middle two numbers is 63, the two middle numbers are 7 and 9.
So the common difference is 2; that makes the 6 numbers
3, 5, 7, 9, 11, 13
You could, of course, solve the problem using algebra; however, it takes far more work than the logical analysis solution shown above.
Let the first term be a and the common difference be d; then the 6 numbers are
a, a+d, a+2d, a+3d, a+4d, a+5d
Then
(1)  the sum of the first and last numbers is 16 the sum of the first and last numbers is 16
(2)  the product of the two middle numbers is 63 the product of the two middle numbers is 63
Solve equation (1) for a: 
Substitute into equation (2):





Substitute back into equation (1) to find a:



I think I like the logical analysis solution better....
Answer by ikleyn(52785)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find six numbers in AP, such that the sum of the two extremes be 16 and the product of the two middle terms be 63.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If the sum of the two extreme terms of the AP is 16, then the sum of any two other terms, equally remoted from the end-terms is 16, too.
It is WELL KNOWN property of any AP, the property which each student should learn when he or she studies the sum of an arithmetic progression.
Hence, in our case, if 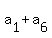 = 16, then = 16, then
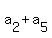 = 16, = 16,
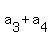 = 16.
Thus we can reformulate the original problem in this way:
Find six numbers in AP, such that the sum of the two middle terms be 16 and the product of the two middle terms be 63.
So, the key moment is to find two number whose sum is 16 and the product is 63.
It is very elementary and standard problem. You can solve it using quadratic equation.
But it admits absolutely elementary MENTAL solution: 63 = 7*9 and 7 + 9 = 16.
Thus we found that = 16.
Thus we can reformulate the original problem in this way:
Find six numbers in AP, such that the sum of the two middle terms be 16 and the product of the two middle terms be 63.
So, the key moment is to find two number whose sum is 16 and the product is 63.
It is very elementary and standard problem. You can solve it using quadratic equation.
But it admits absolutely elementary MENTAL solution: 63 = 7*9 and 7 + 9 = 16.
Thus we found that  = 7 and = 7 and  = 9.
Then the common difference is 9-7 = 2, and the AP is, obviously
3, 5, 7, 9, 11, 13.
By the way, the reversed progression
13, 11, 9, 7, 5, 3
is the solution, too. = 9.
Then the common difference is 9-7 = 2, and the AP is, obviously
3, 5, 7, 9, 11, 13.
By the way, the reversed progression
13, 11, 9, 7, 5, 3
is the solution, too.
SOLVED.
------------------
There is a bunch of lessons on arithmetic progressions in this site:
- Arithmetic progressions
- The proofs of the formulas for arithmetic progressions
- Problems on arithmetic progressions
- Word problems on arithmetic progressions
- Mathematical induction and arithmetic progressions
- One characteristic property of arithmetic progressions
- Solved problems on arithmetic progressions
Also, you have this free of charge online textbook in ALGEBRA-II in this site
- ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lessons are the part of this online textbook under the topic "Arithmetic progressions".
Save the link to this textbook together with its description
Free of charge online textbook in ALGEBRA-II
https://www.algebra.com/algebra/homework/complex/ALGEBRA-II-YOUR-ONLINE-TEXTBOOK.lesson
into your archive and use when it is needed.
|
|
|