SOLUTION: The sum of first four terms of G.P. is 30 and sum of first and last term is 18, then find G.P.

Algebra ->  Sequences-and-series -> SOLUTION: The sum of first four terms of G.P. is 30 and sum of first and last term is 18, then find G.P.      Log On


   

Question 1098693: The sum of first four terms of G.P. is 30 and sum of first and last term is 18, then find G.P.
Answer by Fombitz(32388) About Me  (Show Source):
You can put this solution on YOUR website!
S%5B4%5D=a%5B1%5D%2A%28%281-r%5E4%29%2F%281-r%29%29=30
a%5B1%5D%2Ba%5B4%5D=18
.
.
.
a%5B4%5D=a%5B1%5Dr%5E3
a%5B1%5D%2Ba%5B1%5Dr%5E3=18
a%5B1%5D%281%2Br%5E3%29=18
a%5B1%5D=18%2F%281%2Br%5E3%29
Let's use a substitution for better readability,
x=a%5B1%5D
So then,
x%28%281-r%5E4%29%2F%281-r%29%29=30
x=%2830%281-r%29%29%2F%281-r%5E4%29
and
x=18%2F%281%2Br%5E3%29
So,
+%2830%281-r%29%29%2F%281-r%5E4%29=18%2F%281%2Br%5E3%29+
+30%281-r%29%281%2Br%5E3%29+=18%281-r%5E4%29
+-30r%5E4%2B30r%5E3-30r%2B30=18-18r%5E4+
+-12r%5E4%2B30r%5E3-30r%2B12=0+
-6%282r%5E4-5r%5E3%2B5r-2%29=0
%28r-2%29%28r-1%29%28r%2B1%29%282r-1%29=0
Four r solutions,
r=2
r=1
r=-1
r=1%2F2
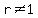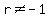We throw out r=1 and r=-1 since the assumption was made when we cross multiplied that r%3C%3E1 and r%3C%3E-1.
So when, r=2,
a%5B1%5D=18%2F%281%2Br%5E3%29
a%5B1%5D=18%2F%281%2B8%29
a%5B1%5D=2
and when r=1%2F2
a%5B1%5D=18%2F%281%2Br%5E3%29
a%5B1%5D=18%2F%281%2B1%2F8%29
a%5B1%5D=18%2F%289%2F8%29
a%5B1%5D=16
So then the geometric progression can be,
{2,4,8,16}
or
{16,8,4,2}