SOLUTION: If a^2,b^2,c^2 are in A.P,show that b+c,c+a,a+b are in H.P.

Algebra ->  Sequences-and-series -> SOLUTION: If a^2,b^2,c^2 are in A.P,show that b+c,c+a,a+b are in H.P.      Log On


   

Question 1083840: If a^2,b^2,c^2 are in A.P,show that b+c,c+a,a+b are in H.P.
Answer by ikleyn(52802) About Me  (Show Source):
You can put this solution on YOUR website!
.
This statement is wrong. 

I will prove it by presenting a counter-example.


Let a = 1, b = 2, c = sqrt%287%29.

Then a%5E2 = 1,  b%5E2 = 4  and  c%5E2 = 7  make an AP.


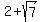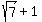Now,  b+c = 2%2Bsqrt%287%29,  c+a = sqrt%287%29%2B1  and  a+b = 1%2B2 = 3.

But these b+c, c+a and a+b DO NOT MAKE a GP.


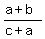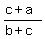To see it, compare the ratios %28a%2Bb%29%2F%28c%2Ba%29  and %28c%2Ba%29%2F%28b%2Bc%29.

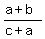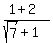We have  %28a%2Bb%29%2F%28c%2Ba%29 = %281%2B2%29%2F%28sqrt%287%29%2B1%29 = 3%2F%28sqt%287%29%2B1%29

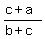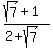   and   %28c%2Ba%29%2F%28b%2Bc%29 = %28sqrt%287%29%2B1%29%2F%282%2Bsqrt%287%29%29,


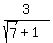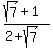and these two fractions/expressions  3%2F%28sqrt%287%29%2B1%29  and  %28sqrt%287%29%2B1%29%2F%282%2Bsqrt%287%29%29  are not equal numbers, as you can easily check.


-----------
Comment from student: We have to prove that it is in H.P not in G.P
-----------


My response: Sorry, my error.
Disregard my post.