Question 1054364: Find the three numbers in an AP such that their sum is 27 and their product is 504
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Answer. a) 4, 9, 14. b) 14, 9, 4.
You may think that there are only two conditions for three unknowns, so the answer is not uniquely defined.
But actually the third condition is that the numbers form AP, and it makes the answer an unique.
Solution
If the members of AP are {a-d), a and (a+d), where a is the middle term and d is the common difference,
then 3a = 27 and a = 9.
Then (a-d)*(a+d) = 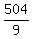 = 56.
Or, in other words, = 56.
Or, in other words, 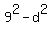 = 56, or = 56, or  = 81-56 = 25.
Then d = +/- 5. = 81-56 = 25.
Then d = +/- 5.
Solved.
|
|
|