Question 1006021: A pronic number is the product of two consecutive positive integers.
110 is a pronic number as 110 = 11 x 10.
The sum of two pronic numbers is 240.
What is the difference between these two numbers?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There may be simpler, more efficient ways to solve this, and I would love to hear about them, but here is what I could come up with.
I would look for two positive integers,  and and  , such that , such that
 and and  are pronic numbers, are pronic numbers,
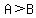 , and , and  . .
Since  ---> --->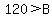 and since and since  , ,  . .
So, the smallest of the two pronic numbers we are looking for is one of the 10 smallest pronic numbers.
BRUTE FORCE SOLUTION:
A brute force solution (trying the first ten pronic numbers) looks feasible.
We could try each of the pronic numbers numbers from  to to 
and see if  is a pronic numbers number . is a pronic numbers number .

With a list of pronic numbers that would be easy.
With a calculator, I would add the digits  to the right of each to the right of each  number, number,
and take the square root to see if it is an integer.
That is a known property of pronic numbers.
I did not know that, but I took the square roots of the  , ,
until I found that  , ,
which is the same as 
I used the fact that if  is pronic, is pronic,
there is a positive integer  such and such and 




 . .
A MORE ELEGANT SOLUTION:
Without a calculator,
I figured I was looking for the  and and  pronic numbers, pronic numbers,
 and and  , ,
with  and and  positive integers, such that positive integers, such that



 . .
So, I need two odd numbers whose squares add to  . .
Since odd numbers' squares end in 1, 5, or 9,
to add up to a sum ending in 2,
both squares should end in 1.
If the  pronic number is the smallest of the two we are looking for, pronic number is the smallest of the two we are looking for,
and we had initially figured out that  , ,
the only possibilities are
 ---> ---> and and  ---> ---> . .
 ---> ---> ---> ---> ---> --->
That gives us the solution:
 and and
 . .
The other choice,
 ---> ---> ---> ---> , ,
does not work, because 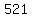 is not a perfect square. is not a perfect square.
|
|
|