Question 564756: The camera has 10.1 million pixels. The product of the pixels across the screen times the pixels up the screen gives the number of pixels the camera has. The ratio of pixels across the screen to pixels up the screen is 4 : 3. How many pixels does this camera have across the screen? Explain what you are calculating as you solve the problem.
Found 8 solutions by Theo, ikleyn, Edwin McCravy, mccravyedwin, n2, AnlytcPhil, n3, greenestamps:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the ratio of horizontal pixels to vertical pixels is 4:3.
let x = the number of horizontal pixels.
let y = the number of vertical pixels.
the ratio of x to y is 4 to 3 which can be shown as:
x/y = 4/3
cross multiply to get:
3x = 4y
solve for y to get:
y = 3x/4
the total number of pixels is 10.1 million.
since the total number of pixels is the number of horizontal pixels times the number of vertical pixels, then your equation would be:
x * y = 10.1
since y = 3x/4, you can substitute for y in this equation to get:
x * 3x/4 = 10.1
simplify this equation to get:
3x^2/4 = 10.1
multiply both sides of this equation by 4 to get:
3x^2 = 40.4
divide both sides of this equation by 3 to get:
x^2 = 13.46666667
take the square root of both sides of this equation to get:
x = 3.669695719
since x * y = 10.1, substitute for x in this equation to get:
3.669695719 * y = 10.1
divide both sides of this equation by 3.669695719 to get:
y = 2.752271789
this suggest that:
the number of horizontal pixels across the screen is 3.669695719 million.
the number of vertical pixels across the screen is 2.752271789.
since the ratio of horizontal pixels to vertical pixels is 4/3, then that ratio should also be equal to 3.669695719 / 2.752271789.
your equation to see if that's true would be:
4/3 = 3.669695719 / 2.752271789.
you would cross multiply to get:
4 * 2.752271789 = 3 * 3.669695719
you would simplify that to get:
11.00908716 = 11.00908716 which suggest that the ratios are the same which means you probably have the right numbers of horizontal pixels and vertical pixels.
you would test that out by multiplying them together to get:
3.669695719 * 2.752271789 = 10.1.
all the numbers check out so that's your answer.
Answer by ikleyn(52856)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The camera has 10.1 million pixels. The product of the pixels across the screen times the pixels up the screen
gives the number of pixels the camera has. The ratio of pixels across the screen to pixels up the screen is 4 : 3.
How many pixels does this camera have across the screen? Explain what you are calculating as you solve the problem.
~~~~~~~~~~~~~~~~~~~~~~~
The " solution " by @Theo is FATALLY WRONG in 39 lines.
I came to bring a correct normal solution to this simple elementary problem.
Let 4x be the number of pixels across the screen.
Then 3x is the number of pixels up the screen.
The total number of pixels in the screen is then (4x)*(3x) = 12x^2.
So, we have this equation
12x^2 = 10.1 million, or 12x^2 = 10,100,000.
Find x from this equation
x =  = 917.4239296.
The number of pixels across the screen is about 4x = 4*917.4239296 = 3669.696.
Round to the closest integer 3670.
Answer. The number of pixel across the screen is about 3670. = 917.4239296.
The number of pixels across the screen is about 4x = 4*917.4239296 = 3669.696.
Round to the closest integer 3670.
Answer. The number of pixel across the screen is about 3670.
Solved.
////////// Below is my comment to the Edwin solution //////////
This morning, I saw Edwin's solution after my solution, which I submitted yesterday.
On the one hand, I was glad that Edwin's solution was close to mine.
From the other side, some aspects in Edwin' solution seem strange to me.
Therefore, I'd like to discuss Edwin' solution, in order for to create clarity in the reader's mind.
First of all, throughout the post, Edwin mistakenly and consistently writes 1010000 for 10.1 million.
It is a typo - it should be read as 10100000 at every appearance.
Edwin should fix this typo, so as not to mislead a reader.
Secondly, while solving the problem, Edwin uses an approach, which is not standard.
He introduces the system of equation, which is correct and quite elementary, but then solves it using
online solver, bypassing standard Algebra methods.
Yes, we live in a free country, and everybody is free to apply a method he wants.
But in teaching Algebra, for such standard elementary system of equations we usually use other simple
algebraic methods (solving by hands) that are standard in teaching.
Why I speak about it - because this site is for teaching Algebra - not for
tutors to demonstrate their superiority. So, traditional Algebra methods
are assumed and should be presented first, as I did in my solution.
Thirdly, Edwin insists that the number 3669.7 should be rounded to 3669, largest whole number
that does not exceed 3669.
This Edwin argument is incorrect, since the standard rounding rules directly dictate to round 3669.7 to 3670.
In whole, I am very pleasant that Edwin practically confirmed my solution (3670 pixels
across the camera against incorrect millions pixels in the post by @Theo - it is why
I developed and presented my solution here).
Thank you, Edwin, for it.
But Edwin performed his intention somewhat awkwardly, so I hasten to correct Edwin's mistakes
to support the right concepts in the reader's mind.
--------------------------
Actually, in this problem, it does not matter, which answer to accept, 3670 or 3669.
Since the number 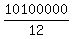 is not a perfect square, we can not expect to get an exact integer value. is not a perfect square, we can not expect to get an exact integer value.
With necessity, we will get some irrational number between two consecutive integer numbers.
Having two possibilities, 3670 and 3669, the better what we can say is that the answer is close to 3670 pixels
across the camera - precisely as I did in my solution.
What is really important, is to apply an adequate approach/method/technique,
be accurate and provide a solution in the frame of a school curriculum,
or as close as possible, in order for the solution be educative.
I would never start debating for such insignificant issue as the difference
between 3670 and 3669 pixels, but Edwin first begun to question my solution.
Thus, I have an obligation to clarify.
\\\\\\\\\ Edwin, it is my response to your response as mccravyedwin /////////
In his response, Edwin writes (I copy-paste)
Ikleyn ignores the fact that there are exceptions to the 'rounding off' rule,:
"Round up if first digit you're dropping is 5 or more" rule, otherwise round
down".
One exception would be that if the question of a problem asks the number of
people that can fit into a room, and your calculation gives 11.9, the answer
would be 11 rather than 12.
The exceptions to that rule are in word problems dealing with things that we
cannot have fractions of, such as people or pixels. We must have whole
numbers of people and pixels.
Therefore, in this problem we must be conservative and round down the number of
pixels, for there is not enough room on the camera to squeeze in one whole extra
pixel.
Answer: 3669, not 3670.
Also, Ikleyn frowns on the use of online technology. I see nothing wrong with it
in solving word problems, for the skill in a word problem is translating English
sentences to algebra sentences (aka equations). That is, setting up the
equations, not solving them.
Edwin
- - - - - - - - Below is my (iKleyn) reasoning - - - - - - - -
It is really interesting point, deserving a discussion.
So, in my solution I got x = 917.4239296, 4x = 4*917.4239296 = 3669.696, and I rounded it to 3670,
following standard rounding rules.
3x = 3*917.4239296 = 2752.272, and I rounded it to 2752,
following standard rounding rules.
Now the product (4x)*(3x) is 3670*2752 = 10099840, and it is less than 10.1 million.
So,  prevents me from claiming that 3670 is the prevents me from claiming that 3670 is the  number of pixels across the camera.
On contrary, if I take the number 3669, then the product (4x)*(3x) will be 3669*2752 = 10097088,
which means that I loose many (2752) pixels for nothing (due to using wrong conception). number of pixels across the camera.
On contrary, if I take the number 3669, then the product (4x)*(3x) will be 3669*2752 = 10097088,
which means that I loose many (2752) pixels for nothing (due to using wrong conception).
This analysis shows that 3670 is  answer than 3669. answer than 3669.
Then we account for greater number of pixels, still being within 10.1 million of pixels.
Thus, you see that the pair (x,y) = (3660,2752) is BETTER than the pair (x,y) = (3669,2752).
For completeness, let's consider the pair (3659,2753). It produces the product
3659*2753 = 10100757, which is greater than 10.1 million of pixels, and therefore does not work in this problem.
So, this analysis shows that the pair (3670,2752) provides the BEST possible answer in this problem.
ANSWER. 3670 is THE  possible number of pixels across the camera in this problem, possible number of pixels across the camera in this problem,
on contrary to Edwin's INCORRECT answer 3669.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by mccravyedwin(408)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn ignores the fact that there are exceptions to the 'rounding off' rule,:
"Round up if first digit you're dropping is 5 or more" rule, otherwise round
down".
One exception would be that if the question of a problem asks the number of
people that can fit into a room, and your calculation gives 11.9, the answer
would be 11 rather than 12.
The exceptions to that rule are in word problems dealing with things that we
cannot have fractions of, such as people or pixels. We must have whole
numbers of people and pixels.
Therefore, in this problem we must be conservative and round down the number of
pixels, for there is not enough room on the camera to squeeze in one whole extra
pixel.
Answer: 3669, not 3670.
Also, Ikleyn frowns on the use of online technology. I see nothing wrong with it
in solving word problems, for the skill in a word problem is translating English
sentences to algebra sentences (aka equations). That is, setting up the
equations, not solving them.
Edwin
Answer by n2(2)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I am @ikleyn. Hello again.
This 'n2' is my second nickname, which I created to place here my response to Edwin's objections.
- - - - - Here I discuss Edwin's arguments, disprove them - - - -
- - - - - - and give the final answer to this problem - - - - - -
It is really interesting point, deserving a discussion.
So, in my solution I got x = 917.4239296, 4x = 4*917.4239296 = 3669.696, and I rounded it to 3670,
following standard rounding rules.
3x = 3*917.4239296 = 2752.272, and I rounded it to 2752,
following standard rounding rules.
Now the product (4x)*(3x) is 3670*2752 = 10099840, and it is less than 10.1 million.
So,  prevents me from claiming that 3670 is the prevents me from claiming that 3670 is the  number of pixels across the camera.
On contrary, if I take the number 3669, then the product (4x)*(3x) will be 3669*2752 = 10097088,
which means that I loose many (2752) pixels for nothing (due to using wrong conception). number of pixels across the camera.
On contrary, if I take the number 3669, then the product (4x)*(3x) will be 3669*2752 = 10097088,
which means that I loose many (2752) pixels for nothing (due to using wrong conception).
This analysis shows that 3670 is  answer than 3669. answer than 3669.
Then we account for greater number of pixels, still being within 10.1 million of pixels.
Thus, you see that the pair (x,y) = (3660,2752) is BETTER than the pair (x,y) = (3669,2752).
For completeness, let's consider the pair (3659,2753). It produces the product
3659*2753 = 10100757, which is greater than 10.1 million of pixels, and therefore does not work in this problem.
So, this analysis shows that the pair (3670,2752) provides the BEST possible answer in this problem.
ANSWER. 3670 is THE  correct possible number of pixels across the camera in this problem, correct possible number of pixels across the camera in this problem,
on contrary to Edwin's INCORRECT answer 3669.
//////////////////////////////////////////////
Regarding next Edwin's declaration about "ikleyn frowns on the use online technology",
I'm just embarrassed to comment on it.
At this forum, I was, probably, first, who started using online computing tools.
I was first who started using here online calculator www.reshish.com for solving
word problems on linear systems of equations for 3x3- matrices.
I used this online solver many times for word problems and especially to show/demonstrate
Gauss-Jordan step by step procedure and so on.
I was first at this forum who systematically used online solvers for statistical calculations
(Binomial distribution and Normal distribution).
I used the online plotting tool DESMOS uncounted number of times to create quickly plots
demonstrating functions or as a solver for finding their intersections, when Desmos works
as a solver for non-linear equations and systems of equations.
Every time as I used it, I instructed and encouraged visitors to use this online plotting tool and calculator.
So, I don't really know, who of the tutors at this forum uses online tools and calculators more than me,
and who more than me at this forum makes visitors familiar with these tools and calculators.
It seems very strange, if Edwin does not know it, visiting this forum so often.
So, the statement by Edwin is far from to be true: as far as the heaven is far from earth.
I never stated that I am against using online technology.
My professional activity during my working years was creating computer programs for numerical
modelling processes in Engineering and Continuum Mechanics. It was the theme of my PhD dissertation.
Programming for computers is another half of my mind.
Edwin came up with this conception, in order for easy disprove it and to present me as a kind of conservative idiot.
In my view, it is unacceptably low level making discussion.
Simply in this  problem the equations are so problem the equations are so  and so and so  that that
using online calculators seems to be inappropriate (brings a slight smile).
Much simpler technique is to reduce the Edwin' system of equations to trivial quadratic equation
and take a square root, as I did.
Edwin's position is in one step from to claim replacing the multiplication table by online calculators.
My position is that using online calculators is good to replace routine job,
which does not develop the student' mind.
But every time, when mental exercises are useful (in this case - reducing the system
of two equations to one primitive quadratic equation in one single variable and solving it by taking square root),
it is a sin for a teacher and a sin for a student not to take advantage of such an opportunity.
This method of teaching as "setting up the equations, not solving them", as Edwin suggests,
is a method of producing mentally retarded disabled people at the exit of the high school.
Answer by AnlytcPhil(1807)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Ikleyn is convinced that there are no exceptions to the "round up and down rule".
She believes it so strongly that she believes a whole pixel can fit in a space
which is only 69.6% of the room necessary for a pixel to fit.
Edwin
PS. She was right that I accidentally typed 1010000 for 10100000, but didn't use
it in my calculation. I corrected it.
Answer by n3(2)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I am @ikleyn. Hello again.
This 'n3' is my third nickname, which I created to place here my response to Edwin's objections.
-------------------------------------------------------------------------------
In his post, Edwin writes "Ikleyn is convinced that there are no exceptions to the "round up and down rule".
I never said that. Edwin attributes here this statement to me, but I never made this statement.
In my previous post i PROVED that
- the pair (3670,2752) provides the product, i.e. the number of pixels,
which is less than 10.1 millions, so these dimensions fit to the problem;
- the pair (3759,2752) provides lesser product, i.e. lesser number of pixels,
than 10.1 millions, so we need to reject this pair;
- the pair (3759, 2753) provides greater product, i.e. greater number of pixels
than 10.1 millions, so we need to reject this pair, too.
Thus, I proved numerically, that my pair (3670,2752) is the best approximation for 10.1 millions pixels
from the bottom, comparing to other possible pairs, and THEREFORE this pair (3670,2752) is the UNIQUE solution
to this problem, giving 3670 as the UNIQUE possible correct answer to the problem.
The exceptions Edwin speaks in his post are irrelevant to my reasoning.
The logic of my solution overcomes his argument.
I simply showed/proved that 3670 pixel across and 2752 pixel up FIT the restriction of 10.1 million pixels
and is the best possible approximation to 10.1 million pixels in this problem.
+----------------------------------------------------------------+
| My statement is that 3670 is correct answer to this problem, |
| while 3669 is not. |
+----------------------------------------------------------------+
And this is all that I state. This is all that I proved.
Looking on the way, as Edwin makes the discussion with me, I see repeating pattern.
Edwin attributes me some statement, which I never did, and then disprove this statement.
This method conducting discussion is well known from the time of ancient Greece,
and it is called DEMAGOGY.
Demagogy is a DISHONEST and UNACCEPTABLE way to conduct a discussion.
It's sad to me to see as Edwin applies it in our discussion again and again.
------------------------------
But it seems that Edwin no longer insists that his solution, " 3669 pixels across the camera " is correct ?
Perhaps, Edwin will admit that the correct answer is " 3670 pixels across the camera " ?
Then we, finally, will be able to complete this discussion . . .
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The problem is not presented well, resulting in squabbling between two of the regular tutors at this forum.
Given that the ratio of pixels horizontally and vertically across the screen is 4:3, the total number of pixels can't be exactly 10.1 million. So there is some rounding being done somewhere.
Assuming that the 4:3 ratio is exact, we need to find a solution in which the total number of pixels is APPROXIMATELY 10.1 million.
4x = # of pixels across the screen
3x = # of pixels top to bottom on the screen


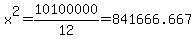
x = approximately=917.4239
Now pixels come in whole numbers, so 4x and 3x must be whole numbers.
If we use x=917, then the total number of pixels is 12x^2 = 10090668, which rounds to 10.1 million.
If we use x=918, then the total number of pixels is 12x^2 = 10112688, which also rounds to 10.1 million.
So the number of pixels across the screen COULD BE (see NOTE below) either 4x = 3668 or 4x = 3672.
The answers 3669 and 3670 from the other two tutors are not correct, because neither of those numbers is a multiple of 4.
---------------------------------------------------------------
NOTE #1: The values x=916 and x=919, resulting in answers of 3664 and 3676 pixels across the screen, also yield total numbers of pixels that round to the given number of 10.1 million.
---------------------------------------------------------------
NOTE #2: And if the 4:3 ratio is NOT exact, then the presentation of the problem is even more unclear....
|
|
|