SOLUTION: Circular logic? (H). Take a Golden Rectangle and draw the largest circle inside it that touches three sides. The circle will touch two opposite sides of the rectangle. If we conn

Algebra ->  Rectangles -> SOLUTION: Circular logic? (H). Take a Golden Rectangle and draw the largest circle inside it that touches three sides. The circle will touch two opposite sides of the rectangle. If we conn      Log On


   

Question 1113279: Circular logic? (H). Take a Golden Rectangle and draw the largest circle
inside it that touches three sides. The circle will touch two opposite sides
of the rectangle. If we connect those two points with a line and then cut
the rectangle into two pieces along that line, will either of the two
smaller rectangles be a Golden Rectangle? Explain your reasoning.
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
The answer to problem as stated is no.  However there is a
similar problem to which the answer is yes. First the problem
as stated is no:

This figure below is drawn to scale. The longer side of the
large rectangle is phi=%28%281%2Bsqrt%285%29%29%2F2%29 times the shorter
side.

  

All golden rectangles are similar.  So the answer is 
no, because neither of those two rectangles is similar
to the large rectangle.

-------------------------------

Now here is a similar problem where the answer is yes.
We draw the line different:

Take a Golden Rectangle and draw the largest circle
inside it that touches three sides. If we draw a line
parallel to the shorter side and tangent to the circle
and then cut the rectangle into two pieces along that
line, will either of the two smaller rectangles be a
Golden Rectangle?
The big rectangle below is Golden.  The short side is "a"
and the long side is 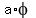a%2Aphi.  The circle is inscribed
in a square. The bottom side of the square is "a" units
So the short side of the small rectangle on the right is 
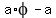
a%2Aphi-a 

 
      |------------------------------------------|
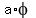                          a%2Aphi

Now we will show that the small rectangle on the right is golden.

The ratio of the sides is

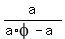a%2F%28a%2Aphi-a%29

Divide numerator and denominator by a

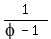1%2F%28phi-1%29

Substitute phi=%28%281%2Bsqrt%285%29%29%2F2%29

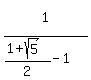1%5E%22%22%2F%28%281%2Bsqrt%285%29%29%2F2-1%29

Multiply top and bottom by 2

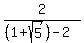
2%2F%28%281%2Bsqrt%285%29%29-2%29

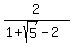
2%2F%281%2Bsqrt%285%29-2%29

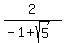2%2F%28-1%2Bsqrt%285%29%29

Rationalize the denominator by multiplying by %28-1-sqrt%285%29%29%2F%28-1-sqrt%285%29%29

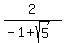
2%2F%28-1%2Bsqrt%285%29%29%22%22%2A%22%22%28-1-sqrt%285%29%29%2F%28-1-sqrt%285%29%29

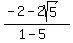
%28-2-2sqrt%285%29%29%2F%281-5%29%29

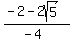
%28-2-2sqrt%285%29%29%2F%28-4%29%29

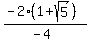%28-2%281%2Bsqrt%285%29%29%29%2F%28-4%29%29

Divide top and bottom by -2:

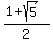%281%2Bsqrt%285%29%29%2F2%29

Which is 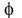phi, the golden ratio.

So for this problem, the answer is 

Yes, the small rectangle on the right is golden.

[I have a hunch this was the problem that was intended.
Point this out to your teacher.]

Edwin