.
1. Make a sketch.
Let ABC be your right-angled triangle with the right angle vertex A.
Let BD and CE be these two medians (|CE| = 2*sqrt(13) and |BD| = sqrt(73), for certainty).
Let x and y be the lengths of the legs AB and AC respectively.
2. From the right triangle ACE and ABD you have
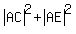 =
=  (1)
(1)
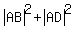 =
= 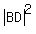 (2)
or
(2)
or
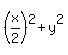 =
=  (3)
(3)
 =
= 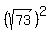 , (4)
By adding equations (3) and (4), you get
, (4)
By adding equations (3) and (4), you get
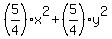 = 4*13 + 73 = 125, or
= 4*13 + 73 = 125, or
 = 100.
3. Thus
= 100.
3. Thus  = 100.
It is the length of the hypotenuse squared,
= 100.
It is the length of the hypotenuse squared, 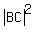 .
Hence, the length of the hypotenuse
.
Hence, the length of the hypotenuse 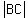 =
=  = 10 cm.
= 10 cm.
Solved. Answer: The length of the hypotenuse is 10 cm.