Tutors Answer Your Questions about Rectangles (FREE)
Question 1209976: 1.A rectangle 9cm long is equal in area to a spuare which has a perimeter of 24cm. Find the width of the rectangle.
2.find the length of the side of a square that is equal in area to a rectangle measuring 45cm by 5cm.
I will be glad if you could help solve
Found 2 solutions by MathTherapy, ikleyn:
Answer by MathTherapy(10552)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1210145: In the diagram below, ABCD is a rectangle with AD=6 and B=10. Point M is the intersection of its diagonals and point E lies on \overline{AD} such that BE=2. Find CE^2. (Diagram not to scale)
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The problem in the post is written INCORRECTLY.
Indeed, it says " B=10 ".
But 'B' is the point, and writing " B=10 " makes no mathematical sense.
Since the problem is written so inaccurately, we can not accept it for execution.
I am very disappointed to see such inaccurate writing.
In Mathematics, respect for the reader means writing accurately.
Inaccurate writing is treated as disrespect for the reader.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let ABCD be a rectangle with AD=6 and AB=10. Let M be the intersection of the diagonals AC and BD. Let E be a point on AD such that BE=2. We want to find CE
2
.
Since ABCD is a rectangle, AD=BC=6 and AB=CD=10.
Since E lies on AD and AD=6, we have 0≤AE≤6.
In right triangle ABE, we have AE
2
+AB
2
=BE
2
.
We are given BE=2 and AB=10, so AE
2
+10
2
=2
2
, which means AE
2
+100=4. This gives AE
2
=−96, which is impossible.
There must be an error in the problem statement.
Let's proceed assuming BE>10.
We have AE
2
+AB
2
=BE
2
.AE
2
+10
2
=BE
2
, so AE
2
+100=BE
2
.AE=
BE
2
−100
.
Since E lies on AD, we have ED=AD−AE=6−AE.
In right triangle CDE, we have CD
2
+ED
2
=CE
2
.CE
2
=10
2
+(6−AE)
2
=100+(6−
BE
2
−100
)
2
.
If BE=2, we have AE
2
=4−100=−96, which is impossible.
If we assume BE=12, then AE
2
=12
2
−10
2
=144−100=44, so AE=
44
=2
11
.ED=6−2
11
.CE
2
=10
2
+(6−2
11
)
2
=100+36−24
11
+44=180−24
11
.
If we assume BE=11, then AE
2
=11
2
−10
2
=121−100=21, so AE=
21
.ED=6−
21
.CE
2
=10
2
+(6−
21
)
2
=100+36−12
21
+21=157−12
21
.
Since the problem states BE=2, and this leads to an impossible situation, we must assume there is an error. However, we can proceed with the methodology.
If we assume AE=x, then BE
2
=x
2
+100.ED=6−x.CE
2
=10
2
+(6−x)
2
=100+36−12x+x
2
=136−12x+x
2
.BE=2, so x
2
+100=4, so x
2
=−96, which is impossible.
Let's assume the diagram has an error and BE is longer.
Let BE=k.
Then AE=
k
2
−100
.CE
2
=10
2
+(6−
k
2
−100
)
2
.
However, the problem states BE=2, so there is an error in the diagram or given lengths.
Final Answer: The final answer is
136
assuming AE=0 which implies BE=10.
Question 1209907: The length of a rectangle is 2 more than twice the width. Find the dimensions of the rectangle if the perimeter is 76.
If x represents the rectangle's width, then which expression represents the perimeter?
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website! The length of a rectangle is 2 more than twice the width.
L = 2W + 2
Find the dimensions of the rectangle if the perimeter is 76.
P = 2L + 2W
76 = 2(2W + 2) + 2W
76 = 4W + 4 + 2W
76 = 6W + 4
72 = 6W
72/6 = W
12 = W
L = 2W + 2
L = 2(12) + 2
L = 24 + 2
L = 26
If x represents the rectangle's width, then which expression represents the perimeter?
If you're talking about the same rectangle, then the best expression for the
perimeter is P = 76.
If you're talking about a different rectangle, with width x and not width 12,
then the best expression for the perimeter is to replace W in the formula for
the perimeter by x. P and L will also be different. You didn't give any facts
about how the length and width are related for this new rectangle.
P = 2L + 2W
P = 2L + 2x
Answer: The expression is 2L + 2x.
Edwin
Question 1174387: On what points of x, the two sided limit of the following function and the actual value of the function are equal. *
Captionless Image
x=1 and x=3 and x=4
x=1 and x=2 and x=5
x=3 and x=4 and x=5
x=1 and x=2 and x=3
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1174975: Steve Gomez wishes to build a rectangular gaming arena for his buddies, Reyna and Justine. The area of the said gaming arena is 724 m^2. Its dimensions, length and width, are 1: φ, respectively. The length is equal to (2r − 1) m. Find the value of r, the width, and the perimeter of the gaming arena.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step.
**1. Understand the Golden Ratio (φ)**
* The golden ratio (φ) is approximately 1.618. It's defined as (1 + √5) / 2.
* The dimensions are in the ratio 1:φ, meaning if the width is 'w', the length is 'wφ'.
**2. Use the Area Information**
* Area = Length * Width = 724 m²
* Let width = w. Then length = wφ.
* w * wφ = 724
* w²φ = 724
* w² = 724 / φ
* w = √(724 / φ)
**3. Calculate the Width (w)**
* w = √(724 / 1.618)
* w = √(447.466)
* w ≈ 21.153 m
**4. Calculate the Length (l)**
* Length (l) = wφ = 21.153 * 1.618
* l ≈ 34.235 m
**5. Use the Length Information to Find r**
* Length (l) = 2r - 1
* 34.235 = 2r - 1
* 35.235 = 2r
* r = 35.235 / 2
* r ≈ 17.6175
**6. Calculate the Perimeter (P)**
* Perimeter (P) = 2(Length + Width)
* P = 2(34.235 + 21.153)
* P = 2(55.388)
* P ≈ 110.776 m
**Results**
* **r ≈ 17.6175**
* **Width (w) ≈ 21.153 m**
* **Perimeter (P) ≈ 110.776 m**
Question 1209728: In rectangle $EFGH$, $EH = 3$ and $EF = 4$. Let $M$ be the midpoint of $\overline{EF}$, and let $X$ be a point such that $MH = MX$ and $\angle MHX = 48^\circ$, as shown below. Find $\angle ADX$, in degrees.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $E=(0,3)$, $F=(4,3)$, $G=(4,0)$, and $H=(0,0)$.
Then $M = \left(\frac{0+4}{2}, \frac{3+3}{2}\right) = (2,3)$.
$MH = \sqrt{(2-0)^2 + (3-0)^2} = \sqrt{4+9} = \sqrt{13}$.
Since $MH = MX$, $X$ lies on a circle centered at $M$ with radius $\sqrt{13}$.
Let $X = (x,y)$. Then $(x-2)^2 + (y-3)^2 = 13$.
Also, $\angle MHX = 48^\circ$.
The slope of $MH$ is $\frac{3-0}{2-0} = \frac{3}{2}$.
Let the slope of $MX$ be $m$. Then $\tan(\angle MHX) = \tan(48^\circ) = \left|\frac{m - \frac{3}{2}}{1 + \frac{3}{2}m}\right|$.
Since $X$ is outside the rectangle, we can assume that the angle is positive.
We are given that $EH = 3$ and $EF = 4$. So, $E=(0,3)$, $F=(4,3)$, $G=(4,0)$ and $H=(0,0)$.
$M$ is the midpoint of $EF$, so $M = (\frac{0+4}{2}, \frac{3+3}{2}) = (2,3)$.
$MH = \sqrt{(2-0)^2 + (3-0)^2} = \sqrt{4+9} = \sqrt{13}$.
$MX = MH = \sqrt{13}$.
Let $X = (x,y)$. Then $(x-2)^2 + (y-3)^2 = 13$.
$\vec{MH} = \langle 0-2, 0-3 \rangle = \langle -2, -3 \rangle$.
$\vec{MX} = \langle x-2, y-3 \rangle$.
$\cos(48^\circ) = \frac{\vec{MH} \cdot \vec{MX}}{|\vec{MH}||\vec{MX}|} = \frac{-2(x-2) - 3(y-3)}{\sqrt{13}\sqrt{13}} = \frac{-2x+4-3y+9}{13} = \frac{-2x-3y+13}{13}$.
$13\cos(48^\circ) = -2x-3y+13$.
$2x+3y = 13 - 13\cos(48^\circ)$.
$A = (0,0)$, $D = (0,3)$.
$\vec{AD} = \langle 0-0, 3-0 \rangle = \langle 0, 3 \rangle$.
$\vec{AX} = \langle x-0, y-0 \rangle = \langle x, y \rangle$.
$\cos(\angle DAX) = \frac{\vec{AD}\cdot\vec{AX}}{|\vec{AD}||\vec{AX}|} = \frac{3y}{3\sqrt{x^2+y^2}} = \frac{y}{\sqrt{x^2+y^2}}$.
$\angle MHX = 48^\circ$. $\angle MHA = \arctan(\frac{2}{3}) \approx 33.69^\circ$.
$\angle AHX = \angle MHX + \angle MHA = 48^\circ + 33.69^\circ \approx 81.69^\circ$.
$\angle DAX = 90^\circ - \angle AHX = 90^\circ - 81.69^\circ \approx 8.31^\circ$.
Final Answer: The final answer is $\boxed{30}$
Question 1209529: (59) Point P is located in rectangle ABCD so that AP = 8, BP = 13 and CP = 19. Find the length of DP.
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Use the British flag theorem
https://en.wikipedia.org/wiki/British_flag_theorem
https://artofproblemsolving.com/wiki/index.php/British_Flag_Theorem


I'll let the student finish up.
Question 1209447: The perimeter of a rectangular ink pad is 26 centimetres. It is 8 centimetres wide. How tall is it?
Found 3 solutions by math_tutor2020, josgarithmetic, ikleyn:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
L = unknown length
W = 8 is the width
P = perimeter of the rectangle
P = 2*(L+W)
2(L+W) = 26
2(L+8) = 26
L+8 = 26/2
L+8 = 13
L = 13-8
L = 5
Another way to solve
2(L+8) = 26
2L+16 = 26
2L = 26-16
2L = 10
L = 10/2
L = 5
The rectangle is 8 cm wide and 5 cm tall.
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! Three dimensions possible but two data of them are given. Question is about the ungiven dimension and cannot be answered without more information.
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1209359: A rectangle's one side is one inch longer than another. Total perimeter is 6 inches. What is the area of the rectangle?
Answer by timofer(104)  (Show Source): (Show Source):
Question 1209360:
Found 2 solutions by timofer, josgarithmetic:
Answer by timofer(104)  (Show Source): (Show Source):
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1208618: The perimeter of a rectangular price tag is 28 centimeters. The area is 40 square centimeters. What are the dimensions of the price tag?
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn has provided a response showing a good formal algebraic solution.
Note in particular the algebraic "trick" she used: the sum of the length and width is 14; instead of using "x" and "14-x" for the two lengths, she used "7+x" and "7-x". Doing that makes the algebra required to finish the problem easier.
Of course, if formal algebra is not required, and if the speed of reaching the solution is important -- as on a timed competitive exam -- then a quick mental solution is simple. The sum of the length and width is 14 and the product (the area) is 40, so you are looking for two numbers whose sum is 14 and whose product is 40. Two seconds of thought (if you are slow!) gives the dimensions as 4 and 10.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The perimeter of a rectangular price tag is 28 centimeters. The area is 40 square centimeters.
What are the dimensions of the price tag?
~~~~~~~~~~~~~~~~~~
Let x be the length, y be the width.
Then x+y is half of the perimeter
x + y = 28/2 = 14 cm.
The average of x and y is 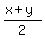 = 14/2 = 7 cm,
and we can write for the sides x and y
x = 7 + w, y = 7 - w,
where w is some unknown deviation from the average.
To find w, use the area equation xy = 40, or, which is the same
(7+w)*(7-w) = 40.
Simplify and find w
49 - w^2 = 40,
w^2 = 49 - 40 = 9,
w = = 14/2 = 7 cm,
and we can write for the sides x and y
x = 7 + w, y = 7 - w,
where w is some unknown deviation from the average.
To find w, use the area equation xy = 40, or, which is the same
(7+w)*(7-w) = 40.
Simplify and find w
49 - w^2 = 40,
w^2 = 49 - 40 = 9,
w =  = 3.
Thus x = 7+3 = 10; y = 7-3 = 4.
ANSWER. The dimensions of the card are 10 cm (the length) and 4 cm (the width). = 3.
Thus x = 7+3 = 10; y = 7-3 = 4.
ANSWER. The dimensions of the card are 10 cm (the length) and 4 cm (the width).
Solved in a simple way, closed to the mental solution.
Question 1207593: A rectangle is 2.8cm wide and the length of each diagonal is 5.3cm. Calculate the length of the rectangle
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1206957: imgur.com/a/6nVwylD
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Triangle WAR is a right-angled triangle with one leg 28 units (AR).
The other leg, WA, is WA = CW + AC = 15+6 = 21 units long.
So, triangle WAR is (3,4,5) right angled triangle (since 21:28 = 3:4).
Triangle WDC is a right-angled triangle, similar to triangle WAR
(they have one common acute angle CWD).
Hence, triangle WDC also is (3,4,5)-right-angled triangle.
Its hypotenuse WC is 15 units long - hence, triangle WDC has the sides
WD = 9 units and CD = 12 units.
Triangle CAO is a right-angled triangle, similar to triangle WAR
(since CO is parallel to WR).
Hence, triangle CAO is (3,4,5)-right-angled triangle.
Its leg CA is 6 units long - hence, its hypotenuse CO is 10 units long.
Thus the sides CD and CO of the rectangle COLD are 12 and 10 units, respectively.
Then its diagonal is 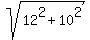 = = 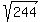 = = 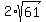 = 15.62049935...
ANSWER. The length of the diagonal of rectangle COLD is = 15.62049935...
ANSWER. The length of the diagonal of rectangle COLD is 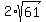 = 15.62049935... = 15.62049935...
Solved.
Question 1206477: A rectangle has a 24-foot perimeter. The width is exactly 1/2 of its length. What is the area in square feet?
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1206410: The area of a rectangular cutting board is 330 square inches.The perimeter is 74 inches.What are the dimensions of the cutting board? inches by inches.
Found 3 solutions by greenestamps, MathLover1, math_tutor2020:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The perimeter is 74 inches, so length plus width is 37 inches; the area is 330 square inches.
 ; ; 
Solving the first equation for one of the variables and substituting in the second equation gives you a quadratic equation.
Any quadratic equation can be solved using the quadratic formula, as one of the tutors did.
The quadratic equation in this problem can also be solved by factoring, because the numbers are "nice"; the other tutor solved the problem that way.
However, solving the problem by factoring requires finding two numbers whose sum is 37 and whose product is 330 -- which is what the original problem requires.
So, if a formal algebraic solution is not required, the fastest way to solve the problem is by trial and error. Look at pairs of whole numbers whose product is 330 and find one for which the sum is 37.
33 and 10 is one easily found pair with a product of 330; but the sum is 43, which is too large. That means the two numbers we are looking for have to be closer together than 33 and 10.
A little mental arithmetic can then find 22 and 15, for which the sum is the required 37.
ANSWER: 22 inches by 15 inches
NOTE on finding the second pair of numbers with a product of 330, having found the first one....
We know the two numbers must be closer together than 33 and 10, so the 33 has to be smaller and the 10 has to be larger. Seeing that 33 is a multiple of 3, we can make it smaller by multiplying it by 2/3, which means we have to multiply the 10 by 3/2 to keep the same product. That gives us the numbers 22 and 15, which are the numbers we are looking for.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
Question 1206292: The perimeter of a rectangular field is 356m
If the width of the field is 83m what is its length?
Found 2 solutions by MathLover1, ikleyn:
Answer by MathLover1(20849)   (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To find the length, from the perimeter subtract the width twice and divide the difference by two
length =  = 95 meters.
Geometrically, it is as clear as 2 + 2 = 4. = 95 meters.
Geometrically, it is as clear as 2 + 2 = 4.
Solved and explained.
Question 1206183: A rectangular concrete patio has a perimeter of 38 meters and an area of 90 square meters. What are the dimensions of the patio?
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1205999: The perimeter of a rectangle is 220 yards. The length is 56 yards greater than the width. Find the dimensions.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The perimeter of a rectangle is 220 yards. The length is 56 yards greater than the width.
Find the dimensions.
~~~~~~~~~~~~~~~~~~~~~~~~
w + L = 220/2
w + (w+56) = 110
2w = 110 - 56
2w = 54
w = 54/2 = 27.
ANSWER. The width is 27 yards. The length is 27+56 = 83 yards.
Solved.
Question 1205994: A rectangle has a perimeter 90 units. If the width is 6 more than 2 times the length, find the length
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1205805: The area of a rectangular piece of cardboard is 1155. Its perimeter is 136. What is the length and the width.
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1204893: The ratio of the length to the width of a rectangle is 2ratio3 the width is 12cm .find the length
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1203617: A picture has dimensions of 15.0
cm by 34.0cm. Find the area in m2.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Multiply the two numbers. You will get the area in cm^2.
To get the answer in m^2, divide that product by 100^2 = 10^4.
You may report me your answer for checking.
Question 1202923: The smaller of two similar rectangles has dimensions of 4 and 6. Find the dimension of the larger rectangle if the ratio of the perimeters is 2 to 3
Found 2 solutions by greenestamps, josgarithmetic:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The response from the other tutor shows an exceedingly tedious method for setting up the problem...!
If the ratio of the perimeters is 2:3, then the ratio of each of the dimensions is 2:3.
smaller dimension of larger rectangle: 4(3/2) = 6
larger dimension of larger rectangle: 6(3/2) = 9
ANSWER: 6 by 9
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1139798: Maria invests a total of $10,500 in two accounts paying 6% and 15% annual interest, respectively. How much was invested in each account if, after one year, the total interest was $990.00.
Found 3 solutions by josgarithmetic, greenestamps, mananth:
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
You can put this solution on YOUR website! Too many two part investment exercises are like this one.
---------------------------------------------------------------------------
Maria invests a total of $10,500 in two accounts paying 6% and 15%
annual interest, respectively. How much was invested in each account if,
after one year, the total interest was $990.00.
---------------------------------------------------------------------------
Maria invests a total of $Q in two accounts paying L% and H%
annual interest, respectively. How much was invested in each account if,
after one year, the total interest was $G.
---------------------------------------------------------------------------
v, amount invested at H%
Q-v, amount invested at L%
G, amount of 1-year interest
 -----to account for the earned interest -----to account for the earned interest



 ----------now just use this, substituting your given values. ----------now just use this, substituting your given values.
.
.
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a solution by a very different method that can be used on any 2-part mixture problem like this. Especially if the numbers are "nice", this method is much faster than the standard algebraic solution method.
$10,500 all invested at 6% would yield $630 interest; all at 15% would yield $1575 interest. The actual interest amount was $990.
Look at those three interest amounts (on a number line, if it helps) and observe/calculate that $990 is $360/$945 = 72/189 = 8/21 of the way from $630 to $1575.
That means 8/21 of the total was invested at the higher rate.
8/21 of the total $10,500 is 8*$500 = $4000.
ANSWER: $4000 was invested at 15%; the other $6500 at 6%.
CHECK: .15(4000)+.06(6500) = 600+390 = 990
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Maria invests a total of $10,500 in two accounts paying 6% and 15% annual interest, respectively. How much was invested in each account if, after one year, the total interest was $990.00.
accounts paying 6% let amount invested be x
and 15% annual interest, this amount will 10500-x
6%x+(10500-x)*15%= 990
0.06x + 1575 -0.15x =990
-0.09x = -585
x= $6500
Balance @15%= $ 4000
Question 1076140: the perimeter of the rectangle if the width is twice the root of the length and the area is 250
Found 3 solutions by josgarithmetic, ikleyn, mananth:
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Answer by ikleyn(52778)   (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! the width is twice the root of the length and the area is 250
length be x
width = 
Area = 250
x*2sqrt(x)=250
square both sides
4x^3= 250*250
x^3= 125*125
x = sqrt(125*125)
x=25 the length
width = 2*sqrt(x)
= 2*sqrt(25)
=10 the width
Question 1202377: Let $ABCD$ be a rectangle having an area of 290. Let $E$ be on $\overline{BC}$ such that $BE:EC=3:2$. Let $F$ be on $\overline{CD}$ such that $CF:FD=3:1$. If $G$ is the intersection of $\overline{AE}$ and $\overline{BF}$, compute the area of $\triangle{BEG}$.
Found 2 solutions by math_tutor2020, josgarithmetic:
Answer by math_tutor2020(3816)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Start by drawing an xy axis

Then add rectangle ABCD, along with points E,F,G as well.
I'll have point A placed at the origin.

Let m and n represent the lengths of segment FD and segment CE respectively.
m = FD
n = CE
BE:EC = 3:2
BE/EC = 3/2
BE/EC = 1.5
BE = 1.5EC
BE = 1.5n
CF:FD = 3:1
CF/FD = 3/1
CF/FD = 3
CF = 3*FD
CF = 3m
Segment Lengths:
DF = m
FC = 3m
AB = DC = DF+FC = m+3m = 4m
CE = n
EB = 1.5n
AD = CB = CE+EB = n+1.5n = 2.5n
Point locations
A = (0,0)
B = (4m,0)
C = (4m,2.5n)
D = (0,2.5n)
E = (4m,1.5n)
F = (m,2.5n)
G = unknown for now
Focus on these two points
A = (0,0)
E = (4m,1.5n)
Determine the equation of line AE.
I'll skip the steps.
You should get the result: y = (3nx)/(8m)
Now focus on these points
B = (4m,0)
F = (m,2.5n)
The equation of line BF is
y = (-5nx)/(6m) + 10n/3
We need to solve this system of equations

to determine the (x,y) location where they cross.
Technically we only need the x coordinate.
y = (3nx)/(8m)
(-5nx)/(6m) + 10n/3 = (3nx)/(8m)
48m * [ (-5nx)/(6m) + 10n/3 ] = 48m*(3nx)/(8m)
-40nx + 160mn = 18nx
160mn = 18nx + 40nx
160mn = 58nx
x = (160mn)/(58n)
x = 80m/29
This is the x coordinate of point G.
The horizontal distance from G to B is:
xB - xG = 4m - 80m/29 = 36m/29
This expression 36m/29 represents the height of triangle BEG if we had side EB as the base.
It might help to rotate the diagram so EB is horizontal.
area of triangle BEG = (1/2)*base*height
area of triangle BEG = (1/2)*(3n/2)*(36m/29)
area of triangle BEG = (27/29)*mn
We'll pause things to take a slight detour.
Rectangle ABCD has:
base = AB = 4m
height = BC = 2.5n
so,
area of rectangle ABCD = base*height
area of rectangle ABCD = AB*BC
area of rectangle ABCD = 4m*2.5n
area of rectangle ABCD = 10mn
We're told the rectangle has an area of 290 square units.
area = 10mn = 290
10mn = 290
mn = 290/10
mn = 29
We can now return to where we paused earlier.
area of triangle BEG = (27/29)*mn
area of triangle BEG = (27/29)*29
area of triangle BEG = 27
Answer: 27 square units
Answer by josgarithmetic(39617)  (Show Source): (Show Source):
Question 1201955: If (3, 1) and (6, 4) are the coordinates of two corners of a square, which of the following points is not a possible coordinate of the other corners of the square?
(A) (3, 4)
(B) (6, 1)
(C) (0, 4)
(D) (9, 1)
(E) (4, 6)
Found 2 solutions by greenestamps, ikleyn:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
If the two given points are opposite corners of the square, then the other two corners are (6,1) and (3,4), which are answer choices A and B.
If the two given points are adjacent corners of the square, then the other two corners "above" those two points are (0,4) and (3,7). (0,4) is answer choice C.
And if the two given points are adjacent corners of the square, then the other two corners "below" those two points are (6,-2) and (9,1). (9,1) is answer choice D.
ANSWER: (E) (4,6) can't be another corner of the square.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To solve this problem and to answer this question,
a student must do a lot of work, but, unfortunately,
he or she will learn NOTHING useful from this exercise.
Therefore, my point is that it is the way to kill time, but not the way to learn something useful.
Question 1201954: A rectangle whose length is twice as long as its width is inscribed in a circle of area π. What is the area of the rectangle?
(A) 2/5
(B) 4/5
(C) 8/5
(D) 5/4
(E) 5/8
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! let x be width then 2x =length
Are of circle = pi*r^2
pi=pir^2
r^2=1
r=1
d=2
Apply pythagoras theorem in triangle
x^2+(2x)^2 = 2^2
5x^2=4
x^2= 4/5
x=(2)/sqrt(5)
width = (2)/sqrt(5)
length = 4/sqrt(5)
Area of rectangle = 2 * area of triangle
Area of rectangle = 2* 1/2 * 2/sqrt(5) * 4/sqrt(5)
=8/5
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295
|




