SOLUTION: Identify the points of discontinuity,holes,vertical asymptotes, and horizontal asmyptotes of each. 1)(x^2+x)/(3x^2-9x) 2)1/x^2-7

Algebra ->  Rational-functions -> SOLUTION: Identify the points of discontinuity,holes,vertical asymptotes, and horizontal asmyptotes of each. 1)(x^2+x)/(3x^2-9x) 2)1/x^2-7      Log On


   

Question 975202: Identify the points of discontinuity,holes,vertical asymptotes, and horizontal asmyptotes of each.
1)(x^2+x)/(3x^2-9x)
2)1/x^2-7
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
%22f%28x%29%22=%28x%5E2%2Bx%29%2F%283x%5E2-9x%29
I'll just do the first one. 

Factor the numerator and denominator:

%22f%28x%29%22=%28x%28x%2B1%29%29%2F%283x%28x-3%29%29

Setting the denominator = 0,  3x(x-3) = 0, tells us that
we have discontinuities at x=0, and at x=3

We must decide which type of discontinuity we have at 0 and 3.

1. If we can cancel a common factor in the numerator and denominator
and remove the discontinuity, then it is a "removable discontinuity" 
or "a hole in the graph".

2. If we can't cancel a factor, then the discontinuity is infinite and 
there is an asymptote there.

We have one of each type.

1. We can remove the discontinuity at x=0 by cancelling the x in the 
numerator and denominator.  To find out where the hole is, we cancel
the x and get a new function which is like the original function everywhere
except at the hole.  Let's call it g(x):

%22g%28x%29%22=%28x%2B1%29%2F%283%28x-3%29%29
%22g%28x%29%22=%28x%2B1%29%2F%283x-9%29%29

g(x) doesn't have a hole at x=0, we substitute and find 
  
%22g%280%29%22=%280%2B1%29%2F%283%280%29-9%29=1%2F%28-9%29%29=-1%2F9

So f(x) has a hole at 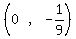%28matrix%281%2C3%2C0%2C%22%2C%22%2C-1%2F9%29%29


2. We cannot remove the discontinuity at x=3 by cancelling, so there is
a vertical asymptote there, a "non-removable" discontinuity.

Since the degree of the numerator and denominator have the same degree, 1,
there is a horizontal asymptote at y = the ratio of the two leading
coefficients, so the horizontal asymptote has equation y=1/3,

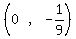So we plot the hole at %28matrix%281%2C3%2C0%2C%22%2C%22%2C-1%2F9%29%29, the vertical asymptote at x=3, and the horizontal 
asymptote at y=1/3:

 
 



Edwin