SOLUTION: 1) The population P of deers at t years is given by P= (2000a^t)/(4+a^t) where a is constant.Given that there are 800 deers in the park after 6 years, a) Find the value of

Algebra ->  Rational-functions -> SOLUTION: 1) The population P of deers at t years is given by P= (2000a^t)/(4+a^t) where a is constant.Given that there are 800 deers in the park after 6 years, a) Find the value of       Log On


   

Question 347820: 1) The population P of deers at t years is given by P= (2000a^t)/(4+a^t)
where a is constant.Given that there are 800 deers in the park after 6 years,
a) Find the value of a to 4 dp (i got 1.1776..is that right?)
b)Use the model to predict the number of years needed for the population of deer to increase from 800 to 1800
c)With reference to this model explain why the population of deer cannot exceed 2000
2)Find the roots A and B where A Thanks
Answer by jsmallt9(3758) About Me  (Show Source):
You can put this solution on YOUR website!
a) "a" = 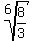root%286%2C+8%2F3%29 which is approximately 1.1776...
This makes your equation: P+=+%282000%2A%28root%286%2C+8%2F3%29%29%5Et%29%2F%284+%2B+%28root%286%2C+8%2F3%29%29%5Et%29

b) First we find the years it takes the population to reach 1800:

Multiply both sides by 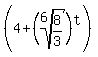%284+%2B+%28root%286%2C+8%2F3%29%29%5Et%29:
7200+%2B+1800%28root%286%2C+8%2F3%29%29%5Et+=+2000%28root%286%2C+8%2F3%29%29%5Et
Subtract 1800%28root%286%2C+8%2F3%29%29%5Et%29 from each side:
7200+=+200%28root%286%2C+8%2F3%29%29%5Et%29
Divide both sides by 200:
36+=+%28root%286%2C+8%2F3%29%29%5Et%29
Find the logarithm of each side, using a base that your calculator "knows":
log%28%2836%29%29+=+log%28%28%28root%286%2C+8%2F3%29%29%5Et%29%29%29
Use the property of logarithms, log%28x%2C+%28p%5Eq%29%29+=+q%2Alog%28x%2C+%28p%29%29, to move the exponent/variable out in front:
log%28%2836%29%29+=+t%2Alog%28%28root%286%2C+8%2F3%29%29%29
Divide both sides by 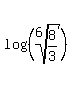log%28%28root%286%2C+8%2F3%29%29%29:
log%28%2836%29%29%2Flog%28%28root%286%2C+8%2F3%29%29%29+=+t
Use your calculator for a decimal approximation:
21.9213625253483390+=+t
This is how long it takes for the population to reach 1800. For the time it takes for the population to increase from 800 to 1800, just subtract the 6 years it took to reach 800: 151.9213625253483390.

c) To answer this part, take the equation:
P+=+%282000%2A%28root%286%2C+8%2F3%29%29%5Et%29%2F%284+%2B+%28root%286%2C+8%2F3%29%29%5Et%29
and multiply the numerator and denominator on the right by: 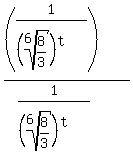. (You'll see why when we're done.)

Multiplying the numerators and using the Distributive Property on the denominators we get:
P+=+2000%2F%284%2F%28%28root%286%2C+8%2F3%29%29%5Et%29+%2B+1%29
With the equation in this form and with some knowledge about how exponents and fractions work we can figure out why the deer population will never exceed 2000:
  • Since t is time it can never be negative. The lowest value it can be is zero. When t = 0, P+=+2000%2F%284%2F%28%28root%286%2C+8%2F3%29%29%5E0%29+%2B+1%29. Since any nonzero number to the zero power is 1 we get: P+=+2000%2F%284%2F1+%2B+1%29+=+2000%2F5+=+400. So the population at t = 0 (IOW the initial population) is 400.
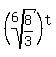  • As t increases, %28root%286%2C+8%2F3%29%29%5Et increases
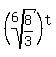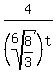  • As %28root%286%2C+8%2F3%29%29%5Et increases, 4%2F%28root%286%2C+8%2F3%29%29%5Et decreases (because as the denominator increases the value of the entire fraction decreases)
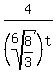  • As 4%2F%28root%286%2C+8%2F3%29%29%5Et decreases, 4%2F%28%28root%286%2C+8%2F3%29%29%5Et%29+%2B+1 decreases
  • As 4%2F%28%28root%286%2C+8%2F3%29%29%5Et%29+%2B+1 decreases, 2000%2F%284%2F%28%28root%286%2C+8%2F3%29%29%5Et%29+%2B+1%29 increases (because as a denominator decreases, the value of the entire fraction increases).
  • So the highest population will come with the highest value of t.
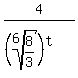  • For very large values of t, the denominator of 4%2F%28%28root%286%2C+8%2F3%29%29%5Et%29 will become an extremely large positive number. And a fraction with a positive numerator and an extremely large positive denominator will be a positive fraction which is very, very close to zero.
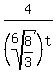  • If 4%2F%28root%286%2C+8%2F3%29%29%5Et is a positive number very close to zero then 4%2F%28%28root%286%2C+8%2F3%29%29%5Et%29+%2B+1 will be a number just a tiny bit above 1.
  • And if 4%2F%28%28root%286%2C+8%2F3%29%29%5Et%29+%2B+1 is a number just barely above 1, then 2000%2F%284%2F%28%28root%286%2C+8%2F3%29%29%5Et%29+%2B+1%29 is a number just barely below 2000.

This is why the population will never exceed 2000. (In fact, since 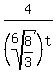4%2F%28root%286%2C+8%2F3%29%29%5Et can never actually be zero, 4%2F%28%28root%286%2C+8%2F3%29%29%5Et%29+%2B+1 can never actually be 1 and the population can never actually be 2000.)