Question 180374: Graph the function y = |x+1|
Found 2 solutions by Mathtut, Electrified_Levi:
Answer by Mathtut(3670)   (Show Source):
You can put this solution on YOUR website! plot points
:
say x=1 then y=abs(x+1) =abs(2)=2
(1,2)
:
say x=-3 then y=abs(x+1)=abs(-2)=2
:
(-3,2)
:
you can plot as many points as you think it takes to get a picture of what the graph will look like
:
hope that helps
Answer by Electrified_Levi(103) (Show Source):
You can put this solution on YOUR website! Hi, Hope I can help,
.
Graph the function y = |x+1|
.
Absolute value is how far the number is on the number line. Absolute value makes any number inside them positive.
.
.
.
.
Knowing this principle
.
.
We know that "y" will always be positive, since "y" equals an absolute value
.
All absolute value graphs look like a "V", the very point that the two lines meet will always be where "y" equals "0" ( since "0" is neither positive or negative, it doesn't have absolute value ), the "V" goes out from this point
.
Let us graph a few points
.
.
First we replace "x" with any number
.
We will replace "x" with (-1)
.
=  =  ,
.
.
.
Points are given as (x,y)
.
Our point is ( -1,0 )
.
.
We need to find at least two more points to make the graph, we need a point with "x" as a positive number, and one with "x" as a negative number
.
We will replace "x" with "5"
.
=  = 
.
.
.
Our point is (x,y), ( 5,6 )
.
.
We will now replace "x" with a negative number
.
We will replace "x" with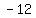 
.
=  = 
.
 ( since absolute value makes all negatives positive )
.
.
.
Our point is (x,y) , ( -12,11 )
.
.
We could now draw the equation, by drawing a line from ( -1,0 ) to ( -12, 11 ) then keep drawing the line after ( -12 , 11 ), then we would draw a line from (-1,0) to (5,6) and beyond
.
We could find more points if we wanted to,
.
"x" as (-7), =  = 
.
( absolute value )
.
.
Our point is ( -7,6 )
.
.
"x" as "10", =  = 
.
.
.
Our point is (10,11)
.
.
Here is the graph
.
.
(for some reason graph doesn't make a complete "V" for some reason, don't worry )
.
Hope I helped, Levi
|
|
|
