Question 1200349: Evaluate the piecewise defined function at the indicated values.
f(x) = {4x if x<-4
{ x+2 If -4<_ x <_ 5
{ (x-5)^2 if x > 5
f(-5)=
f(-4)=
f(4)=
f(5)=
f(8)=
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Answers:
f(-5)= -20
f(-4)= -2
f(4)= 6
f(5)= 7
f(8)= 9
Explanation:
Piecewise functions are a Frankenstein of sorts because they have multiple functions glued together.
Another way to look at it is that the piecewise function has split identities.
The input x will determine which piece to use.- If
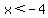 , then , then  - If
 , then , then  - If
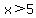 , then , then 
If the input is x = -5, then we go for the interval 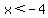 . Draw out a number line to see why this is the case. . Draw out a number line to see why this is the case.
This means we pick the first piece.



If the input is x = -4, then we go for the interval 
This time we go for the 2nd piece.



We stick with the 2nd piece for the input x = 4, since it is also in the interval 



Same goes for x = 5



The last input x = 8 will involve the third piece, since we're now in the interval 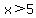




This is what the piecewise graph looks like

The first piece 4x is in red. It is graphed only when 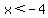
The second piece x+2 is in green. It is graphed only when 
The third piece (x-5)^2 is in blue. It is graphed only when 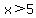
There are open holes at (-4, -16) and (5, 0)
The open holes are not part of the graph. Think of them as potholes in the road.
There are closed filled in endpoints at (-4, -2) and (5, 7)
I recommend either Desmos or GeoGebra as two graphing options.
Here's the link to the interactive Desmos graph
https://www.desmos.com/calculator/jkfomczjuz
This will allow you to zoom in/out, move the window around, etc.
|
|
|