Question 1132381: The straight line 3x-4y-3=0 cuts the circle x^2+y^2-4x-2y+4=0. Find (i)the coordinates of its centre (ii)the radius (iii)equations of tangent and normal to this circle from the origin
Found 2 solutions by Alan3354, ikleyn:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! The straight line 3x-4y-3=0 cuts the circle x^2+y^2-4x-2y+4=0. Find (i)the coordinates of its centre (ii)the radius (iii)equations of tangent and normal to this circle from the origin
----------------
Find (i)the coordinates of its centre
x^2+y^2-4x-2y+4=0
x^2+y^2-4x-2y = -4
x^2-4x + y^2-2y = -4
Complete the squares for x and y:
x^2-4x+4 + y^2-2y+1 = -4+4+1 = 1
(x-2)^2 + (y-1)^2 = 1
Center at (2,1)
======================
(ii)the radius
r = 1
======================
(iii)equations of tangent and normal to this circle from the origin
One tangent is the x-axis, or y = 0.
---
The distance from the Origin to (2,1) is sqrt(5).
Label the Origin O, the center C, the tangent point P, and the point (2,0) T.
Angle CPO is 90 degs.
OC = sqrt(5)
CP = 1, the radius of the circle.
OP = 2
----------------
Slope of OC = 1/2 = tangent of the angle between the x-axis and OC
Triangles OCP and OCT are congruent --> angle COT = and COP = arctan(1/2)
Slope of OP = tan(2*tan(POC)) = 4/3
y = 4x/3 is the 2nd tangent line.
===================
Not clear what you mean by the lines normal, and I don't see how the given line is relevant.
Answer by ikleyn(52788)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The normal to the circle from the origin is the straight line from the origin (0,0) through the center (2,1).
Its equation is y = 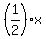 . .
|
|
|