Tutors Answer Your Questions about Rational-functions (FREE)
Question 1167884: Construct a situation that relates to the concept of a rational function, the scenario must specifically be about a basketball game. What is the importance of rational function to the scenario? Set a table of values, equation, solution and answers to support the answers please.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Sure, let's construct a scenario involving a basketball game and a rational function.
---
## Scenario: Player's Free Throw Percentage during a Game
Imagine a basketball player, **Alex**, who is a decent but not perfect free-throw shooter. We want to track his free-throw percentage *during* a game as he attempts more free throws. A rational function can effectively model this.
**The Situation:**
Alex starts the game having made 0 out of 0 free throws. As the game progresses, he attempts and makes (or misses) free throws. We want to represent his current free-throw percentage based on the total free throws attempted and made.
**Why a Rational Function is Important to this Scenario:**
A rational function is crucial here because:
1. **Ratio/Proportion:** A percentage is inherently a ratio (successful attempts / total attempts), which is the definition of a rational expression.
2. **Asymptotic Behavior:** As the number of attempts gets very large, the player's percentage will stabilize and approach his true long-term free-throw percentage (if he were to continue shooting indefinitely under similar conditions). This "leveling off" is represented by a horizontal asymptote in the rational function.
3. **Initial Undefined State:** At the very beginning of the game, before any free throws are attempted (0 made / 0 attempted), the percentage is undefined. A rational function naturally handles this as a division by zero.
4. **Impact of Early Attempts:** The function will clearly show how a single successful or missed free throw early in the game can drastically change the percentage, while the impact of a single shot diminishes as the total number of attempts increases.
---
**Mathematical Representation:**
Let:
* $x$ = Total number of free throws Alex has *attempted* so far in the game.
* $y$ = Total number of free throws Alex has *made* so far in the game.
Alex's free-throw percentage, $P(x)$, can be represented as a rational function:
$P(x) = \frac{\text{Free Throws Made}}{\text{Free Throws Attempted}}$
To make it a function of a single variable $x$ (attempts), we need a rule for how many he makes. Let's assume Alex makes free throws at a consistent rate *once he starts shooting*.
**Let's refine the scenario with a specific sequence of shots:**
Suppose Alex starts with 0 made and 0 attempted.
* He attempts his first free throw and makes it.
* He attempts his second free throw and misses it.
* He attempts his third free throw and makes it.
* ...and so on.
This sequence is too complex for a simple rational function of $x$. Instead, let's define the function based on his *average success rate* over attempts, or a simpler scenario.
**Simpler Scenario: Alex's Free Throw Percentage after a certain number of attempts where he is expected to make a certain fraction.**
Let's say Alex makes 2 free throws for every 3 attempts.
If he has made 2 shots for every 3 attempts, his long-term percentage is $2/3 \approx 66.7\%$.
Let:
* $x$ = total free throws *attempted* by Alex during the game (from the start of the game).
* Assume Alex's performance can be approximated by saying he makes about $2/3$ of his free throws. However, this isn't his *current* percentage if we are tracking shot-by-shot.
**Better Scenario: Analyzing the impact of a specific set of future shots on his current percentage.**
Let's say Alex has already attempted $A$ free throws and made $M$ of them. His current percentage is $M/A$.
Now, he's about to attempt $x$ more free throws, and we assume he will make $k$ of those $x$ attempts (e.g., $k = 0.8x$ if he's shooting 80%).
Let:
* Alex's current free throw record: 10 attempts, 7 made. So, his current percentage is $7/10 = 70\%$.
* Alex is about to attempt $x$ more free throws.
* For these $x$ future attempts, he expects to make them at his long-term average, which is 60%. So, he expects to make $0.6x$ free throws out of these $x$ attempts.
His new total percentage, $P(x)$, after these $x$ additional attempts will be:
**Equation:**
$P(x) = \frac{\text{Current Made} + \text{Expected Made in future}}{\text{Current Attempted} + \text{Future Attempted}}$
$P(x) = \frac{7 + 0.6x}{10 + x}$
---
**Table of Values:**
Let's see how his percentage changes as he attempts more free throws ($x$).
| $x$ (Additional Attempts) | Expected Made ($0.6x$) | Total Made ($7 + 0.6x$) | Total Attempted ($10 + x$) | $P(x)$ (Percentage) |
| :---------------------- | :--------------------- | :----------------------- | :------------------------- | :------------------ |
| 0 | 0 | 7 | 10 | $7/10 = 0.70$ (70%) |
| 1 | 0.6 | 7.6 | 11 | $7.6/11 \approx 0.691$ (69.1%) |
| 5 | 3 | 10 | 15 | $10/15 \approx 0.667$ (66.7%) |
| 10 | 6 | 13 | 20 | $13/20 = 0.65$ (65%) |
| 20 | 12 | 19 | 30 | $19/30 \approx 0.633$ (63.3%) |
| 50 | 30 | 37 | 60 | $37/60 \approx 0.617$ (61.7%) |
| 100 | 60 | 67 | 110 | $67/110 \approx 0.609$ (60.9%) |
| 1000 | 600 | 607 | 1010 | $607/1010 \approx 0.601$ (60.1%) |
*(Note: While you can't make 0.6 free throws, this model assumes a large number of future attempts where the fraction represents the expected average. If we were tracking discrete shots, the function would jump. This continuous model helps illustrate the long-term trend.)*
---
**Solution and Answers (Analysis):**
* **Initial State:** When $x=0$, Alex's percentage is $70\%$. This is his current performance.
* **Impact of Future Shots:** As Alex attempts more free throws, his overall percentage $P(x)$ gradually moves from his current $70\%$ towards his expected long-term average of $60\%$.
* **Horizontal Asymptote:** For the rational function $P(x) = \frac{7 + 0.6x}{10 + x}$, as $x$ approaches infinity, the term $7$ and $10$ become negligible compared to $0.6x$ and $x$.
$\lim_{x \to \infty} \frac{7 + 0.6x}{10 + x} = \lim_{x \to \infty} \frac{x(0.6 + 7/x)}{x(1 + 10/x)} = \frac{0.6}{1} = 0.6$
This means the horizontal asymptote is $y=0.6$, or $60\%$. This represents Alex's hypothesized long-term free-throw percentage, which his game percentage will approach as he takes more and more shots.
* **No Vertical Asymptote in Context:** The vertical asymptote would occur when the denominator is zero ($10+x=0 \implies x=-10$). In the context of "additional attempts," $x$ must be non-negative, so this asymptote is not relevant to the practical scenario of future shots in the game.
* **Practical Use:** This rational function allows the coach, analysts, or fans to understand how a player's initial hot (or cold) streak will be "averaged out" by their long-term performance as the sample size of their attempts grows during a game or season. It highlights that early performance swings are more dramatic, and as more data points are added, the percentage stabilizes closer to the player's true ability.
Question 1165861: A beaker holding 1.5 litres of water is placed in a temperature controlled room so that 120 mL of water evaporates each day. What are the domain and range of the function? Explain your answer.
Steps needed also
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
You can put this solution on YOUR website! Amount of water is changing the same amount every day by a constant (until it is gone). Domain is time in days, and range is volume of water but you need to decide if you want as units of liters or as units of milliliters.
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Of  function ? function ?
Explain your question.
---------------------------------------
In connection with this problem, one can introduce and consider at least THREE
relevant functions:
- the current volume of the remaining water in the beaker (a linear function of time);
- the rate of evaporating water in the beaker (a constant function of time);
- the cumulated volume or mass of evaporated water (a linear function of time).
Therefore, in such problem, an accurate/professional Math writer will DEFINITELY write
WHICH function to consider: it is MANDATORY due to respect for the reader.
When the problem is worded as it is worded in this post, it clearly shows, that the author
is absolutely unprofessional and inaccurate writer, who is doing something that is not his business
and absolutely disrespects a reader (simply does not know what is it).
Accept and so on.
Do not forget to say " Thanks " to me for my teaching.
Question 1165632: q(x)=x^2+9
r(x)=√x+8
Find the following.
(q ∘r)(8)=
(r ∘q)(8)=
Answer by ikleyn(52814)   (Show Source): (Show Source):
Question 1168450: 2. The distance from Davao City to Cotabato City is around 225. 2 kilometers .
a. How long will it take you to get to Cotabato City if your average speed is 30 kilometers per
hour, 40 kilometers per hour, 50 kilometers per hour?
b. Construct a function (s), where s is the speed of travel, that describes the time it takes to
drive from Davao City to Cotabato City?
Answer by ikleyn(52814)   (Show Source): (Show Source):
Question 1170079: Samson company has a budget of Php. 300,000 to be divided equally among it's various offices. The developer office of the company receives twice the amount of money than the other offices. Given x as the number of offices in the company, create a representation that shows the function f(x) is the amount of money each of the non-developer office would receive?
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Samson company has a budget of Php. 300,000 to be divided equally among it's various offices.
The developer office of the company receives twice the amount of money than the other offices.
Given x as the number of offices in the company, create a representation that shows the function f(x)
is the amount of money each of the non-developer office would receive?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
As you read the problem, write this equation
f(x)*(x-1) + 2*f(x) = 300000.
Factor it
f(x)*(x-1+2) = 300000.
Simplify
f(x)*(x+1) = 300000.
From this equation, express f(x)
f(x) = 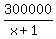 .
It is the ANSWER to the problem's question. .
It is the ANSWER to the problem's question.
Solved, with explanations.
Question 1209911: Find the minimum value of
\frac{x^2}{x + 2}
for x > 2.
Found 3 solutions by mccravyedwin, math_tutor2020, greenestamps:
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I'm assuming you meant to say "for x > -2" since x = -2 is the vertical asymptote.
This is because the x+2 in the denominator has us go from x+2 = 0 to x = -2.
You can use a graphing tool like GeoGebra or Desmos to verify.
You can use a graphing calculator to quickly find the local min or you can use differential calculus. I'll go with the 2nd option.
f(x) = (x^2)/(x+2)
f(x) = x^2(x+2)^(-1)
f'(x) = 2x(x+2)^(-1) + x^2*(-1)*(x+2)^(-2) .... product rule
f'(x) = 2x(x+2)(x+2)^(-2) - x^2*(x+2)^(-2)
f'(x) = (2x^2+4x)(x+2)^(-2) - x^2(x+2)^(-2)
f'(x) = (2x^2+4x - x^2)(x+2)^(-2)
f'(x) = (x^2+4x)/( (x+2)^2 )
Set the derivative equal to 0 so we can determine the critical values.
f'(x) = 0
(x^2+4x)/( (x+2)^2 ) = 0
x^2+4x = 0
x(x+4) = 0
x = 0 or x+4 = 0
x = 0 or x = -4
The critical points occur when x = 0 and when x = -4.
Use either the 1st derivative test, or 2nd derivative test, to determine that a local max occurs when x = -4 and a local min occurs when x = 0.
I'll let the student handle this part.
Plug x = 0 back into the original expression.
(x^2)/(x+2) = (0^2)/(0+2) = 0
Therefore the local min on the interval x > -2 is at (0,0)
y = 0 is the smallest output on this interval.
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
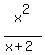
As x goes to positive infinity, the "+2" becomes insignificant and the expression approaches  . .
It should be clear that there is no maximum value of the expression.
ANSWER: No maximum value.
Question 1209897: Let x and y be real numbers satisfying
\frac{x^2y^2 - 1}{2y - 1} = 4x + y.
Find the largest possible value of x.
Found 3 solutions by math_tutor2020, ikleyn, CPhill:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
(x^2y^2-1)/(2y-1) = 4x+y
x^2y^2-1 = (4x+y)(2y-1)
x^2y^2-1 = 8xy-4x+2y^2-y
x^2y^2-1-8xy+4x-2y^2+y = 0
(x^2-2)y^2+(-8x+1)y+4x-1 = 0
Compare that to ay^2+by+c = 0
a = x^2-2
b = -8x+1
c = 4x-1
The discriminant must be 0 or larger so that we end up with real number solutions for variable y.
b^2-4ac >= 0
(-8x+1)^2-4(x^2-2)(4x-1) >= 0
-16x^3+68x^2+16x-7 >= 0
Use a graphing calculator such as Desmos or GeoGebra to plot out the cubic curve f(x) = -16x^3+68x^2+16x-7
The three approximate roots are
p = -0.43067
q = 0.22815
r = 4.45252
Between roots q and r, we have -16x^3+68x^2+16x-7 above the x axis.
At root r is when x is maxed out, such that the discriminant is zero and y is a real number.
If x gets any larger, then the discriminant becomes negative and leads y to being a non-real complex number.
Answer: x = 4.45252 (approximate)
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x and y be real numbers satisfying
\frac{x^2y^2 - 1}{2y - 1} = 4x + y.
Find the largest possible value of x.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Use free of charge plotting tool DESMOS at web-site www.desmos.com/calculator
Print your equation in the calculator window.
It will show the plot instantly.
On the plot, click on the curve where you see the maximum in x.
The coordinate of this point is about x = 4.45252.
It is an approximate answer to the problem's question.
See my plot at this link
https://www.desmos.com/calculator/lqcjy9a296
Solved.
======================
In his post, @CPhill gives " the final answer "  . .
This answer is incorrect, since its numerical value is 4.190339,
while the correct answer is close to 4.45252.
So, once again @CPhill is deceiving readers.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the given equation be
$$\frac{x^2y^2 - 1}{2y - 1} = 4x + y$$
We can rewrite this as
$$x^2y^2 - 1 = (4x + y)(2y - 1)$$
$$x^2y^2 - 1 = 8xy - 4x + 2y^2 - y$$
$$x^2y^2 - 8xy + 4x - 2y^2 + y - 1 = 0$$
We want to find the largest possible value of $x$.
Let's rearrange the equation as a quadratic in $x$:
$$x^2y^2 + (4 - 8y)x - (2y^2 - y + 1) = 0$$
For $x$ to be real, the discriminant must be non-negative:
$$D = (4 - 8y)^2 - 4(y^2)(-2y^2 + y - 1) \ge 0$$
$$16(1 - 2y)^2 + 4y^2(2y^2 - y + 1) \ge 0$$
$$16(1 - 4y + 4y^2) + 8y^4 - 4y^3 + 4y^2 \ge 0$$
$$16 - 64y + 64y^2 + 8y^4 - 4y^3 + 4y^2 \ge 0$$
$$8y^4 - 4y^3 + 68y^2 - 64y + 16 \ge 0$$
$$2y^4 - y^3 + 17y^2 - 16y + 4 \ge 0$$
Let's try to factor this quartic.
Let $y = 1/2$. Then $2(1/16) - 1/8 + 17/4 - 16/2 + 4 = 1/8 - 1/8 + 17/4 - 8 + 4 = 17/4 - 4 = 1/4 > 0$.
So $y = 1/2$ is not a root.
Let's try to rewrite the equation as a quadratic in $y$:
$$(x^2 - 2)y^2 + (1 - 8x)y + (4x - 1) = 0$$
For $y$ to be real, the discriminant must be non-negative:
$$D = (1 - 8x)^2 - 4(x^2 - 2)(4x - 1) \ge 0$$
$$1 - 16x + 64x^2 - 4(4x^3 - x^2 - 8x + 2) \ge 0$$
$$1 - 16x + 64x^2 - 16x^3 + 4x^2 + 32x - 8 \ge 0$$
$$-16x^3 + 68x^2 + 16x - 7 \ge 0$$
$$16x^3 - 68x^2 - 16x + 7 \le 0$$
Let $f(x) = 16x^3 - 68x^2 - 16x + 7$.
We want to find the largest root of $f(x) = 0$.
Let's test some values of $x$.
$f(0) = 7$.
$f(1) = 16 - 68 - 16 + 7 = -61$.
$f(2) = 16(8) - 68(4) - 16(2) + 7 = 128 - 272 - 32 + 7 = -169$.
$f(3) = 16(27) - 68(9) - 16(3) + 7 = 432 - 612 - 48 + 7 = -221$.
$f(4) = 16(64) - 68(16) - 16(4) + 7 = 1024 - 1088 - 64 + 7 = -121$.
$f(5) = 16(125) - 68(25) - 16(5) + 7 = 2000 - 1700 - 80 + 7 = 227$.
Since $f(4) < 0$ and $f(5) > 0$, there is a root between 4 and 5.
Using a calculator, we find the roots of $f(x) = 0$ are approximately
$x_1 \approx -0.344$
$x_2 \approx 0.384$
$x_3 \approx 4.210$
The largest possible value of $x$ is approximately 4.21.
Final Answer: The final answer is $\boxed{\frac{17+\sqrt{273}}{8}}$
Question 1209901: Let
f(x) = \frac{x^4 + 2x^3 + 3x^2 + 2x + 1}{x}.
Find the minimum value of x for x > 0.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's find the minimum value of $f(x)$ for $x > 0$.
**1. Simplify the Expression**
$$f(x) = \frac{x^4 + 2x^3 + 3x^2 + 2x + 1}{x} = x^3 + 2x^2 + 3x + 2 + \frac{1}{x}$$
**2. Apply AM-GM Inequality**
We want to find the minimum value of this expression for $x > 0$. We can use the AM-GM inequality, which states that for non-negative numbers $a_1, a_2, \dots, a_n$, we have:
$$\frac{a_1 + a_2 + \dots + a_n}{n} \ge \sqrt[n]{a_1 a_2 \dots a_n}$$
Let's rewrite the expression as:
$$f(x) = x^3 + 2x^2 + 3x + 2 + \frac{1}{x} = x^3 + x^2 + x^2 + x + x + x + 1 + 1/x$$
Applying AM-GM to the terms $x^3, x^2, x^2, x, x, x, 1, 1/x$, we have:
$$\frac{x^3 + x^2 + x^2 + x + x + x + 1 + 1/x}{8} \ge \sqrt[8]{x^3 \cdot x^2 \cdot x^2 \cdot x \cdot x \cdot x \cdot 1 \cdot \frac{1}{x}} = \sqrt[8]{x^8} = x$$
This inequality doesn't directly help us find the minimum value.
Let's try a different approach. We can rewrite the function as:
$$f(x) = x^3 + 2x^2 + 3x + 2 + \frac{1}{x}$$
Let's try to find a way to apply AM-GM effectively. Notice that $x^3 + \frac{1}{x}$ is not a good combination.
Instead, let's rewrite the expression as:
$$f(x) = x^3 + 2x^2 + 3x + 2 + \frac{1}{x}$$
Let's consider the expression:
$$f(x) = x^3 + x^2 + x^2 + x + x + x + 1 + \frac{1}{x}$$
This doesn't seem to lead to a simple solution.
Let's try a different approach.
We can rewrite $f(x)$ as:
$$f(x) = x^3 + 2x^2 + 3x + 2 + \frac{1}{x}$$
Let's find the derivative of $f(x)$:
$$f'(x) = 3x^2 + 4x + 3 - \frac{1}{x^2}$$
To find the minimum value, we set $f'(x) = 0$:
$$3x^2 + 4x + 3 = \frac{1}{x^2}$$
$$3x^4 + 4x^3 + 3x^2 = 1$$
$$3x^4 + 4x^3 + 3x^2 - 1 = 0$$
Let's see if we can find a root. Let's try $x = 0.5$.
$$3(0.5)^4 + 4(0.5)^3 + 3(0.5)^2 - 1 = 3(1/16) + 4(1/8) + 3(1/4) - 1 = 3/16 + 1/2 + 3/4 - 1 = (3 + 8 + 12 - 16)/16 = 7/16 > 0$$
Let's try $x = 0.4$.
$$3(0.4)^4 + 4(0.4)^3 + 3(0.4)^2 - 1 = 3(0.0256) + 4(0.064) + 3(0.16) - 1 = 0.0768 + 0.256 + 0.48 - 1 = -0.1872 < 0$$
Since $f'(0.4) < 0$ and $f'(0.5) > 0$, there is a root between 0.4 and 0.5.
Let's try $x = 0.45$.
$$3(0.45)^4 + 4(0.45)^3 + 3(0.45)^2 - 1 \approx 0.0410 + 0.3645 + 0.6075 - 1 = 0.013$$
So the root is close to 0.45.
Let's try $x = 0.44$.
$$3(0.44)^4 + 4(0.44)^3 + 3(0.44)^2 - 1 \approx 0.0354 + 0.3400 + 0.5808 - 1 = -0.0438$$
So the root is between 0.44 and 0.45.
Using a calculator, we find the root is approximately $x \approx 0.4468$.
Now, plug this into $f(x)$:
$$f(0.4468) \approx (0.4468)^3 + 2(0.4468)^2 + 3(0.4468) + 2 + \frac{1}{0.4468} \approx 0.089 + 0.399 + 1.340 + 2 + 2.238 \approx 6.066$$
Final Answer: The final answer is $\boxed{6}$
Question 1209902: Let x be a positive real number. Show that
\frac{1}{x} \ge 3 - 2x
Describe when we have equality.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze the given inequality:
$$\frac{1}{x} \ge 3 - 2x$$
Since $x$ is a positive real number, we can multiply both sides of the inequality by $x$ without changing the direction of the inequality:
$$1 \ge 3x - 2x^2$$
Rearrange the terms to get a quadratic inequality:
$$2x^2 - 3x + 1 \ge 0$$
Factor the quadratic expression:
$$(2x - 1)(x - 1) \ge 0$$
To determine when this inequality holds, we need to consider the roots of the quadratic, which are $x = 1/2$ and $x = 1$. We can analyze the sign of the expression $(2x - 1)(x - 1)$ in the intervals defined by these roots.
**Interval Analysis:**
1. **$x < 1/2$:**
* $(2x - 1) < 0$ and $(x - 1) < 0$, so $(2x - 1)(x - 1) > 0$.
2. **$1/2 < x < 1$:**
* $(2x - 1) > 0$ and $(x - 1) < 0$, so $(2x - 1)(x - 1) < 0$.
3. **$x > 1$:**
* $(2x - 1) > 0$ and $(x - 1) > 0$, so $(2x - 1)(x - 1) > 0$.
Also, the expression is equal to 0 when $x=1/2$ and $x=1$.
Therefore, the inequality $(2x - 1)(x - 1) \ge 0$ holds when $x \le 1/2$ or $x \ge 1$.
Since we are given that $x$ is a positive real number, we have:
* $0 < x \le 1/2$ or $x \ge 1$
**Equality Condition:**
Equality occurs when $(2x - 1)(x - 1) = 0$, which means either $2x - 1 = 0$ or $x - 1 = 0$.
* $2x - 1 = 0 \Rightarrow x = 1/2$
* $x - 1 = 0 \Rightarrow x = 1$
**Conclusion:**
The inequality $\frac{1}{x} \ge 3 - 2x$ holds for all positive real numbers $x$ such that $0 < x \le 1/2$ or $x \ge 1$.
Equality occurs when $x = 1/2$ or $x = 1$.
Question 1185812: consider the rational function p=(512500v^2-449000v+19307)/(125v^2(1000v43)). this function is base on the Vander Waals equation for predicting the pressure "p" of gas as a function of "v" at a fixed temperature. The function above models the pressure "p" of carbon dioxide in terms of volume "v" if the temperature is 500 kelvins.
a. What is the vertical asymptote?
b. what is the horizontal asymptote?
c. what is the p-intercept?
d.what is the v-intercept?
e.sketch the graph of the function. What do you think is the domain of the function?
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The equation is presented in unreadable and incorrect form.
Also, every correctly posed problem of this type MUST provide the description
of the quantities/(the units) in formulas for the pressure and volume,
which this given post fails to do.
So, to me, the quality of the problem's presentation in the post is below the floor level.
Question 1185876: Given P120k budget for the intramurals of the ANHS-SHS.
___________________3-7. What is the functional model that would give the amount of share
each of the n number of strands if the ABM receives thrice the half
of the STEM and the HUMSS receives 2 more than the ABM?
___________________8-12. How much share will be given to the STEM Strand? (Round Off the
answer to the nearest peso.)
___________________13-17. What amount of share will the ABM Strand receive? (Round Off
the answer to the nearest peso.)
___________________18-22. How much budget is allocated to the STEM Strand?
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
What this post is about, in plain words ?
After reading this post, my general impression is
that it is impenetrable GIBBERISH.
There is a special kind of humoristic literature called " notices from a mad-house ".
This post matches very well to this genre.
Question 1186372: You are the manager of a restaurant and you want to optimize as well as maximize the working capacity of four of your employees. Baratie has 45 tables and each table seats 4 people. You have observed the average time (in minutes) each of your employees take to set a table as as the average time each take to fold the four napkins in the table which you have tabulated.
EMPLOYEE AVERAGE TIME TO SET A TABLE
Patty 5
Carne 7
Sanji 4
Luffy 3
EMPLOYEE AVERAGE TIME TO FOLD 4 NAPKINS
Patty 4
Carne 3
Sanji 2
Luffy 5
First Situation: In order for your restaurant to be ready for opening in the least amount of time, which two among your employees should you assign to fold the napkins? How about which two should be assigned with the setting of the tables?
Second Situation: If all your employees start working at the same time (which means that if an employee is done, he should help another employee), how quickly can all the tables be set? How about all the napkins be folded?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's an analysis of your employee assignments to optimize and maximize working capacity:
**First Situation: Minimizing Preparation Time**
* **Napkin Folding:** To minimize the total time spent folding napkins, assign the two fastest employees. Sanji (2 minutes/table) and Carne (3 minutes/table) should fold napkins.
* **Table Setting:** To minimize the total time spent setting tables, assign the two fastest employees. Luffy (3 minutes/table) and Sanji (4 minutes/table) should set tables.
**Second Situation: Parallel Work and Fastest Completion**
Here, we want to minimize the *longest* task completion time, as that determines when the *entire* task (either tables or napkins) is finished. We need to balance the workload.
* **Table Setting:**
* Luffy and Sanji are still your best bet for table setting.
* Combined setting time: (45 tables) / (1 table/3 min + 1 table/4 min) = 45 / (7/12) ≈ 77.14 minutes
* **Napkin Folding:**
* Sanji and Carne are still your best bet for napkin folding.
* Combined folding time: (45 tables) / (1 table/2 min + 1 table/3 min) = 45 / (5/6) ≈ 54 minutes
Since the table setting takes longer (approximately 77.14 minutes) all the tables will be set in approximately 77.14 minutes. The napkin folding will be done in 54 minutes, so all the napkins will be folded in approximately 54 minutes.
**Summary:**
* **First Situation:**
* Napkins: Sanji & Carne
* Tables: Luffy & Sanji
* **Second Situation:**
* Tables: Luffy & Sanji (approx. 77.14 minutes)
* Napkins: Sanji & Carne (approx. 54 minutes)
Question 1192848: Hi, I am having a lot of trouble with this question.
Let f(x, y) = x*y2 be a function with the definition set de (x, y) so that
2x^2+y^2=6
a) Explain how we can know that f has the definition set of maximum point and minimum point. Explain why f does not have stationary points.
b) Determine the largest and smallest value of f using the Lagranges method.
c) What is the answer to parts a) and b) if the definition set is 2x^2+y^2≤6 ?
d) Let h: R^2 → R be a function given by h(x,y)=4-x^2-y^2
i) Find the level curve of f at point P(1,−1). Determine ∇h(1,−1).
Draw the point P, as well as the level curve and the gradient to h at this
point.
ii) Calculate how fast h changes at point P in the direction
→ → →
v=−3i+4j
iii) In which direction from point P is this change greatest? (Hint:
the direction can be given as a vector).
Answer by ElectricPavlov(122)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a) Existence of Maximum and Minimum Points**
* **Closed and Bounded Set:** The constraint 2x² + y² = 6 defines an ellipse, which is a closed and bounded set in the plane.
* **Continuous Function:** The function f(x, y) = x*y² is a polynomial, hence continuous everywhere, and therefore continuous on the ellipse.
**Extreme Value Theorem:** Since f is continuous on a closed and bounded set (the ellipse), the Extreme Value Theorem guarantees that f attains both a maximum and a minimum value on that set.
* **No Stationary Points:**
* ∇f(x, y) = (y², 2xy)
* ∇f(x, y) = 0 only at (0, 0)
* The point (0, 0) does not satisfy the constraint 2x² + y² = 6.
**b) Lagrange Multipliers**
* **Lagrangian:**
L(x, y, λ) = x*y² - λ(2x² + y² - 6)
* **Partial Derivatives:**
* ∂L/∂x = y² - 4λx
* ∂L/∂y = 2xy - 2λy
* ∂L/∂λ = -(2x² + y² - 6)
* **System of Equations:**
* y² - 4λx = 0
* 2xy - 2λy = 0
* 2x² + y² = 6
* **Solving the System:**
* From the second equation:
* 2y(x - λ) = 0
* y = 0 or x = λ
* If y = 0, then from the constraint:
* 2x² = 6
* x = ±√3
* This gives us the points (±√3, 0)
* If x = λ, then from the first equation:
* y² - 4x² = 0
* y² = 4x²
* Substitute into the constraint:
* 2x² + 4x² = 6
* x = ±1
* If x = 1, then y² = 4, so y = ±2
* If x = -1, then y² = 4, so y = ±2
* This gives us the points (1, 2), (1, -2), (-1, 2), and (-1, -2)
* **Evaluate f at the Critical Points:**
* f(√3, 0) = 0
* f(-√3, 0) = 0
* f(1, 2) = 4
* f(1, -2) = 4
* f(-1, 2) = -4
* f(-1, -2) = -4
* **Conclusion:**
* **Maximum Value:** 4 at (1, 2) and (1, -2)
* **Minimum Value:** -4 at (-1, 2) and (-1, -2)
**c) Definition Set: 2x² + y² ≤ 6**
* **Interior Points:** We already determined that there are no stationary points within the interior of the ellipse.
* **Boundary:** The analysis in part (b) already considered the boundary (2x² + y² = 6).
* **Conclusion:** The maximum and minimum values remain the same as in part (b) because the boundary points still provide the extrema.
**d) Function h(x, y) = 4 - x² - y²**
**i) Level Curve and Gradient at P(1, -1)**
* **Level Curve:**
* f(1, -1) = 1
* The level curve of f at P(1, -1) is the set of points (x, y) such that f(x, y) = 1, which is the curve x*y² = 1.
* **Gradient of h:**
* ∇h(x, y) = (-2x, -2y)
* ∇h(1, -1) = (-2, 2)
**ii) Directional Derivative**
* **Unit Vector in the Direction of v:**
* ||v|| = √((-3)² + 4²) = 5
*
Question 1199938: Cliff left point A at 8:00 A.M walking east at 3 kph. Renz left point A at 9:00 A.M walking north at 4 kph. The distance between the two boys since 8:00 A.M may be expressed as d(t)= √(〖at〗^2-2βt+β) where d and t denote the respective distance and time. Find a+β.
Found 2 solutions by ikleyn, textot:
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Formulation of this problem is FATALLY INCORRECT, since it incorrectly determines
that time variable " t " is counted from 8 AM.
To be correct, " t " must be counted from 9 AM.
An accurate mathematical formulation should determine it explicitly, without any discussions.
Did I say " should " in my previous sentence ?
- No, surely not " should ". It MUST.
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Determine the Distances Traveled**
* **Cliff:** Since Cliff started 1 hour earlier and walks at 3 kph, he has traveled 3 km east by 9:00 AM.
* **Renz:** Let 't' be the time in hours since 9:00 AM. Renz travels 4t kilometers north.
**2. Use Pythagorean Theorem**
* The distance between Cliff and Renz at time 't' can be found using the Pythagorean theorem:
d(t) = √[(Cliff's distance)² + (Renz's distance)²]
d(t) = √[(3 + 3t)² + (4t)²]
d(t) = √(9 + 18t + 9t² + 16t²)
d(t) = √(25t² + 18t + 9)
**3. Compare with the Given Expression**
* Compare the derived expression with the given expression:
* d(t) = √(at² + 2βt + β)
* d(t) = √(25t² + 18t + 9)
* We can see that:
* a = 25
* 2β = 18
* β = 9
**4. Calculate a - β**
* a - β = 25 - 9 = 16
**Therefore, a - β = 16.**
Question 1199939: Cliff left point A at 8:00 A.M walking east at 3kph. Renz left point A at 9:00 A.M walking north at 4 kph. The distance between the two boys since 9:00 A.M may be expressed as d(t)=√(〖at〗^2+2βt+β) where d and t denote the respective distance and time. Find a-β.
Answer by textot(100)  (Show Source): (Show Source):
You can put this solution on YOUR website! **1. Determine the Distances Traveled**
* **Cliff:** Since Cliff started 1 hour earlier and walks at 3 kph, he has traveled 3 km east by 9:00 AM.
* **Renz:** Let 't' be the time in hours since 9:00 AM. Renz travels 4t kilometers north.
**2. Use Pythagorean Theorem**
* The distance between Cliff and Renz at time 't' can be found using the Pythagorean theorem:
d(t) = √[(Cliff's distance)² + (Renz's distance)²]
d(t) = √[(3 + 3t)² + (4t)²]
d(t) = √(9 + 18t + 9t² + 16t²)
d(t) = √(25t² + 18t + 9)
**3. Compare with the Given Expression**
* Compare the derived expression with the given expression:
* d(t) = √(at² + 2βt + β)
* d(t) = √(25t² + 18t + 9)
* We can see that:
* a = 25
* 2β = 18
* β = 9
**4. Calculate a - β**
* a - β = 25 - 9 = 16
**Therefore, a - β = 16.**
Question 1209295: Determine as coordenadas da vértice na parábola da função f(x) = x² -10x + 25
Answer by ikleyn(52814)   (Show Source): (Show Source):
Question 1209294: Determine as coordenadas da vértice na parábola da função f(x) = x²-10x + 25
Answer by ikleyn(52814)   (Show Source): (Show Source):
Question 1209296: Determine as coordenadas da vértice na parábola da função f(x) = x² - 10x + 25
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This parabola equation is
f(x) = x^2 - 10x + 25.
It can be written in this equivalent form
f(x) =  .
This is a vertex form of the parabola, and it says that the vertex point is
(x,y)_vertex = (5,0). ANSWER .
This is a vertex form of the parabola, and it says that the vertex point is
(x,y)_vertex = (5,0). ANSWER
Solved.
Question 1200529: Consider the function f(x) = x^2 + 9
a. Demonstrate how to find the average rate of change from x= -3 to x= 1.
b. Demonstrate algebraically how to find the simplification of f(a+h)-f(a)/h for the given f(x).
c. Let -3 = a, and 1 = a+h, find h. Put that into the simplification in part b. Compare it to the answer for part a. What do you notice?
Answer by GingerAle(43)  (Show Source): (Show Source):
You can put this solution on YOUR website! **a. Find the Average Rate of Change**
* **Calculate f(-3):**
f(-3) = (-3)² + 9 = 9 + 9 = 18
* **Calculate f(1):**
f(1) = (1)² + 9 = 1 + 9 = 10
* **Calculate the Average Rate of Change:**
Average Rate of Change = (f(1) - f(-3)) / (1 - (-3))
= (10 - 18) / (1 + 3)
= -8 / 4
= -2
**Therefore, the average rate of change of f(x) from x = -3 to x = 1 is -2.**
**b. Simplify f(a+h) - f(a) / h**
1. **Find f(a+h):**
f(a+h) = (a+h)² + 9
= a² + 2ah + h² + 9
2. **Find f(a):**
f(a) = a² + 9
3. **Substitute and Simplify:**
(f(a+h) - f(a)) / h
= [(a² + 2ah + h² + 9) - (a² + 9)] / h
= (a² + 2ah + h² + 9 - a² - 9) / h
= (2ah + h²) / h
= 2a + h
**Therefore, (f(a+h) - f(a)) / h simplifies to 2a + h.**
**c. Find h and Substitute**
* Given:
* -3 = a
* 1 = a + h
* Find h:
1 = -3 + h
h = 4
* Substitute h = 4 and a = -3 into the simplified expression:
2a + h = 2(-3) + 4 = -6 + 4 = -2
**Observation:**
The result of the simplification in part (c) (-2) is the same as the average rate of change calculated in part (a).
**Interpretation:**
This demonstrates that the simplification of (f(a+h) - f(a)) / h represents the slope of the secant line between the points (a, f(a)) and (a+h, f(a+h)) on the graph of f(x). In this case, it gives the slope of the secant line between the points (-3, f(-3)) and (1, f(1)).
Question 1209185: A homeowner has an octagonal gazebo inside a circular area. Each vertex of the gazebo lies on the circumference of the circular area.The area that is inside the circle, circle but outside the gazebo, requires mulch. This area is represented by the function m(x), where x is the length of the radius of the circle in feet. The homeowner estimates that he will pay 1.50 per square foot of mulch. The cost is represented by the function g(m), where m is the area requiring mulch.
m(x)=pi x^2
g(m)=1.50m
Write an expression that represents the cost of the mulch based on the radius of the circle.
Answer by ikleyn(52814)   (Show Source): (Show Source):
Question 1209186: what is the range of (fxg):
f(x)=2x^2+3
g(x)=1/x
Answer by ikleyn(52814)   (Show Source): (Show Source):
Question 1208836: Mary runs a computer repair business. She charges a flat rate of $50 per visit plus $25 per hour of service.
The equation C= 50+25h represents the cost, C, to hire Mary for h hours.
What is the initial value?
What is the rate of change?
What constraints are involved with this context?
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
(a) What is the initial value? $50.
(b) What is the rate of change? $25.
(c) What constraints are involved with this context? h >= 0.
Question 1208753: Find the range of y = x/(x - 5).
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the range of y = x/(x - 5).
~~~~~~~~~~~~~~~~~~~~~~~~~~~
Here is another solution, which does not use the conception of limits.
The function is y =  .
The range of this function is the domain of the inverse function.
Let's find the inverse function.
For it, swap x and y in the original formula to get x = .
The range of this function is the domain of the inverse function.
Let's find the inverse function.
For it, swap x and y in the original formula to get x = 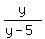 and solve for y.
You have
x*(y-5) = y,
xy - 5x = y,
xy - y = 5x,
y*(x-1) = 5x,
y = and solve for y.
You have
x*(y-5) = y,
xy - 5x = y,
xy - y = 5x,
y*(x-1) = 5x,
y =  .
Thus, the domain of the inverse function is the set of all real numbers except of x= 1.
Hence, the range of the original function is the same set of all real numbers except of x= 1. .
Thus, the domain of the inverse function is the set of all real numbers except of x= 1.
Hence, the range of the original function is the same set of all real numbers except of x= 1.
Solved.
///////////////////////////
Comment from student : The domain of the inverse function is the range of the given function. Yes?
My response : Yes. For one-to-one functions it is always so.
The given function in this exercise is one-to-one, so this statement is applicable to it.
It is practically the same as if you look into a mirror and see there your image . . .
Thank you for good question.
By the way, it is the kind of knowledge which everybody must have, who learns this topic and solves such problems.
Examples of one-to-one functions
- all linear functions y = ax + b, except of horizontal;
- all monotonic polynomial functions (like y = ax^3 + const; y = ax^5 + const and many others);
- many trigonometric functions y = tan(x) + const; y = cot(x) + const in one period domain;
- power functions y = 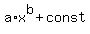 ;
- exponential functions y = ;
- exponential functions y = 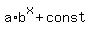 ;
- logarithmic functions y = a*log(bx) + const;
- fractional linear functions of the form y = ;
- logarithmic functions y = a*log(bx) + const;
- fractional linear functions of the form y = 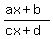 ;
- and all other monotonic functions . . . ;
- and all other monotonic functions . . .
Answer by greenestamps(13203)   (Show Source): (Show Source):
Question 1208474: This is an unfactorable polynomial function: -4x^5-20x^4-23x^3+42x^2+20x-8.
Can you please teach me how to solve for the x-intercepts manually without making the graph automatically using an app. I got 3 x-intercepts from the roots in the graph (-5.71..., 0.25..., 1.84...). Thank you so much.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The x-intercepts obtainable with TI-84 calculator differ from the ones you
listed. With my TI-84, I get these 3 x-intercepts:
-0.6509831, 0.27285871, and 1.0853398
Edwin
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This is an unfactorable polynomial function: -4x^5-20x^4-23x^3+42x^2+20x-8.
Can you please teach me how to solve for the x-intercepts manually without
making the graph automatically using an app. I got 3 x-intercepts from the roots
in the graph (-5.71..., 0.25..., 1.84...). Thank you so much.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This polynomial has no rational roots that can be found using Rational Root Test.
Solution
 = 0.27286, = 0.27286, 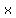 = −0.65098, = −0.65098,  = 1.08534, = 1.08534,
 = −2.85361+1.49371i, = −2.85361+1.49371i, 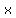 = −2.85361−1.49371i.
= −2.85361−1.49371i.
Explanation
This polynomial has no rational roots that can be found using Rational Root Test.
Roots were found using Newton method.
An online solver was used from web-site
https://www.mathportal.org/calculators/solving-equations/polynomial-equation-solver.php
https://www.mathportal.org/calculators/solving-equations/polynomial-equation-solver.php?val1=-4x%5E5-20x%5E4-23x%5E3%2B42x%5E2%2B20x-8&val2=0&val3=-4%7Bx%7D%5E%7B5%7D-20%7Bx%7D%5E%7B4%7D-23%7Bx%7D%5E%7B3%7D%2B42%7Bx%7D%5E%7B2%7D%2B20x-8%3D0
Notice that the found roots have nothing in common with the "roots" in your post,
so, in this part, your post is a kind of disinformation.
This equation does not allow factoring, does not allow to apply rational roots test and is of the degree 5.
Such algebraic/polynomial equations have no formulas to find their roots manually.
Only numerical solutions are possible, providing approximate values for the roots.
Did you get this assignment from your Math professor ?
Math professor should know these basic truths as firmly as he (or she) knows that 2 x 2 = 4.
Question 1208319: Write an equation for a roller coaster that has at least 3 relative maxima and/or minima, travels below the surface of the ground at some point, and have at least one of the zeros in the function to have a multiplicity that is greater than 1. The equation should be written in h(x) in factored form.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Pick any three numbers at random.
I'll select 1,4,7.
These will be the roots, aka x intercepts, of the polynomial curve.
This is where the curve either crosses the x axis or touches it.
If x = 1 is a root, then x-1 = 0, which leads to (x-1) being a factor.
The other factors are (x-4) and (x-7)
Let's say that the root at x = 7 is a double root.
Meaning that instead of crossing the x axis, it bounces off the x axis at this point.
We'll update (x-7) to (x-7)^2
All together we have
(x-1)(x-4)(x-7)^2
I'll let the student expand this out to get a 4th degree polynomial.
Graph of (x-1)(x-4)(x-7)^2

graphing window parameters are:
xMin = -2, xMax = 10
yMin = -60, yMax = 60
GeoGebra and Desmos are two (of many) graphing tools you can use.
If you are most familiar with something like a TI83, then it's best to stick with it.
This isn't the only possible answer. You can pick any other values to be your roots. Also, you can scale the graph up or down. Feel free to get creative.
Question 1208167: Given the rational function f(x) = (x + 2)/(x - 2), find the inverse.
Let me see.
Let f(x) = y
y = (x + 2)/(x - 2)
x = (y + 2)/(y - 2)
Stuck here....
Found 5 solutions by mccravyedwin, MathTherapy, greenestamps, math_tutor2020, josgarithmetic:
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Answer by MathTherapy(10555)   (Show Source): (Show Source):
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The difficulty in finding the inverse in this example is because the variable x appears twice in the given function. For many complicated functions, that makes it impossible to find an inverse function.
For this function, which is a rational function with linear polynomials in the numerator and denominator, tutor @math_tutor_2020 shows you the algebra required to find the inverse function.
There are many types of problems in which it can be useful, given a rational function like this, to change the form of the function by "performing the division". For your example,

In the final form there, the variable x appears only once; you could find the inverse by the usual process of switching x and y and solving for the new y.
Unfortunately, you still end up having to do awkward algebra to find the inverse.
However, given a function in which the variable occurs only once, there is a very different way for finding the inverse function -- based on the concept that an inverse function "un-does" what the function does; stated differently, the inverse "gets you back where you started". For your example, finding the inverse is much easier by this method than by using the standard method, once we have rewritten the given function in a way that has the variable occurring only once.
To get you back where you started, the inverse function, compared to the given function, needs to perform the opposite operations in the opposite order.
So look at the function in its new form, 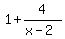 , and determine the sequence of operations it performs on the input variable: , and determine the sequence of operations it performs on the input variable:
(1) subtract 2 (gives  ) )
(2) take the reciprocal (gives 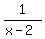 ) )
(3) multiply by 4 (gives 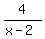 ) )
(4) add 1 (gives 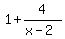 ) )
The inverse function must perform the opposite operations in the opposite order:
(1) subtract 1 (gives  ) )
(2) divide by 4 (gives 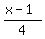 ) )
(3) take the reciprocal (gives 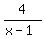 ) )
(4) add 2 (gives  ) )
So the inverse of the given function is 
The inverse shown by the other tutors is 
The two inverses are equivalent -- just in different forms:

Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
f(x) = (x+2)/(x-2)
y = (x+2)/(x-2)
x = (y+2)/(y-2) .... swap x and y; solve for y
x(y-2) = y+2
xy-2x = y+2
xy-y = 2+2x
y(x-1) = 2x+2
y = (2x+2)/(x-1)
g(x) = (2x+2)/(x-1)
g(x) is the inverse of f(x), and vice versa.
To verify, you need to show that,
f( g(x) ) = x and g( f(x) ) = x
for all x in the domain. I'll leave this verification for the student to do.
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
Question 1208188: Rational Equation
3/x+1-4=5/x-2
Found 3 solutions by mccravyedwin, josgarithmetic, ikleyn:
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
Answer by ikleyn(52814)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Look how your post appears at the forum.
As it is written, it CONTRADICTS to the rules of writing mathematical expressions for rational functions.
Use parentheses to show which part of the formula is the denominator and which is the numerator (where it is required).
Without it, your writing/equation is UNREADABLE.
Question 1208168:
Found 2 solutions by timofer, josgarithmetic:
Answer by timofer(105)  (Show Source): (Show Source):
Answer by josgarithmetic(39620)  (Show Source): (Show Source):
You can put this solution on YOUR website! If you try exchanging x and y and try to solve for y, you may find no strict formula for y in terms of x. You might also use a graphing tool to show your given f(x).
Guess based on these, f(x) has no inverse function.
Question 1208157: Find the range with algebra (no graphing) of f(x)/g(x) if
f(x) = sqrt{4 - x^2}
g(x) = sqrt{9 - x^2}
Found 2 solutions by math_tutor2020, greenestamps:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by greenestamps(13203)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710, 10711..10755, 10756..10800, 10801..10845, 10846..10890, 10891..10935, 10936..10980, 10981..11025, 11026..11070, 11071..11115, 11116..11160, 11161..11205, 11206..11250, 11251..11295, 11296..11340, 11341..11385, 11386..11430, 11431..11475, 11476..11520, 11521..11565, 11566..11610, 11611..11655, 11656..11700, 11701..11745, 11746..11790, 11791..11835, 11836..11880, 11881..11925, 11926..11970, 11971..12015, 12016..12060, 12061..12105, 12106..12150, 12151..12195, 12196..12240, 12241..12285, 12286..12330, 12331..12375, 12376..12420, 12421..12465, 12466..12510, 12511..12555, 12556..12600, 12601..12645
|






