SOLUTION: √432 in lowest radical form

Algebra ->  Radicals -> SOLUTION: √432 in lowest radical form      Log On


   

Question 340456: √432 in lowest radical form
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

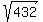sqrt%28432%29 Start with the given expression



The goal of simplifying expressions with square roots is to factor the radicand into a product of two numbers. One of these two numbers must be a perfect square. When you take the square root of this perfect square, you will get a rational number.


So let's list the factors of 432


Factors:
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 27, 36, 48, 54, 72, 108, 144, 216, 432


Notice how 144 is the largest perfect square, so lets factor 432 into 144*3


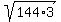sqrt%28144%2A3%29 Factor 432 into 144*3


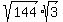sqrt%28144%29%2Asqrt%283%29 Break up the square roots using the identity sqrt%28x%2Ay%29=sqrt%28x%29%2Asqrt%28y%29


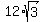12%2Asqrt%283%29 Take the square root of the perfect square 144 to get 12


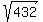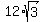
So the expression sqrt%28432%29 simplifies to 12%2Asqrt%283%29

----------------------------
Check:
Notice if we evaluate the square root of 432 with a calculator we get

sqrt%28432%29=20.7846096908265

and if we evaluate 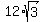12%2Asqrt%283%29 we get

12%2Asqrt%283%29=20.7846096908265

This shows that sqrt%28432%29=12%2Asqrt%283%29. So this verifies our answer