Tutors Answer Your Questions about Radicals (FREE)
Question 1209888: Compute
\frac{\{\sqrt{3}\} - 4 \{\sqrt{5}\}}{\{\sqrt{3}\}^2 + \{\sqrt{2}\}^2}.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's compute the given expression step-by-step.
**Understanding Fractional Parts**
The fractional part of a number $x$, denoted by $\{x\}$, is defined as $\{x\} = x - \lfloor x \rfloor$, where $\lfloor x \rfloor$ is the greatest integer less than or equal to $x$.
**Calculating Fractional Parts**
1. **$\{\sqrt{3}\}$:**
* $\sqrt{3} \approx 1.732$
* $\lfloor \sqrt{3} \rfloor = 1$
* $\{\sqrt{3}\} = \sqrt{3} - 1$
2. **$\{\sqrt{5}\}$:**
* $\sqrt{5} \approx 2.236$
* $\lfloor \sqrt{5} \rfloor = 2$
* $\{\sqrt{5}\} = \sqrt{5} - 2$
3. **$\{\sqrt{2}\}$:**
* $\sqrt{2} \approx 1.414$
* $\lfloor \sqrt{2} \rfloor = 1$
* $\{\sqrt{2}\} = \sqrt{2} - 1$
**Substituting into the Expression**
Now, substitute these fractional parts into the given expression:
$$\frac{\{\sqrt{3}\} - 4 \{\sqrt{5}\}}{\{\sqrt{3}\}^2 + \{\sqrt{2}\}^2} = \frac{(\sqrt{3} - 1) - 4(\sqrt{5} - 2)}{(\sqrt{3} - 1)^2 + (\sqrt{2} - 1)^2}$$
**Simplifying the Numerator**
* $(\sqrt{3} - 1) - 4(\sqrt{5} - 2) = \sqrt{3} - 1 - 4\sqrt{5} + 8 = \sqrt{3} - 4\sqrt{5} + 7$
**Simplifying the Denominator**
* $(\sqrt{3} - 1)^2 = (\sqrt{3})^2 - 2\sqrt{3} + 1 = 3 - 2\sqrt{3} + 1 = 4 - 2\sqrt{3}$
* $(\sqrt{2} - 1)^2 = (\sqrt{2})^2 - 2\sqrt{2} + 1 = 2 - 2\sqrt{2} + 1 = 3 - 2\sqrt{2}$
* $(\sqrt{3} - 1)^2 + (\sqrt{2} - 1)^2 = (4 - 2\sqrt{3}) + (3 - 2\sqrt{2}) = 7 - 2\sqrt{3} - 2\sqrt{2}$
**Putting it Together**
The expression becomes:
$$\frac{\sqrt{3} - 4\sqrt{5} + 7}{7 - 2\sqrt{3} - 2\sqrt{2}}$$
**Approximating the Result**
Let's approximate the values:
* $\sqrt{3} \approx 1.732$
* $\sqrt{5} \approx 2.236$
* $\sqrt{2} \approx 1.414$
Numerator:
* $1.732 - 4(2.236) + 7 = 1.732 - 8.944 + 7 = -0.212$
Denominator:
* $7 - 2(1.732) - 2(1.414) = 7 - 3.464 - 2.828 = 0.708$
Then the fraction is:
$$\frac{-0.212}{0.708} \approx -0.299435$$
**Exact Result**
$$\frac{\sqrt{3} - 4\sqrt{5} + 7}{7 - 2\sqrt{3} - 2\sqrt{2}}$$
Final Answer: The final answer is $\boxed{\frac{7 + \sqrt{3} - 4 \sqrt{5}}{7 - 2 \sqrt{2} - 2 \sqrt{3}}}$
Question 1209873: Find all x such that
sqrt{3x^2 + 2x + 1} + sqrt{3x^2 + 2x - 3} = 20.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find all x such that
sqrt{3x^2 + 2x + 1} + sqrt{3x^2 + 2x - 3} = 20.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Let u = 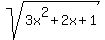 , v = , v =  are new variables.
Then for new variables we have this system of equations
u + v = 20, (1)
u^2 - v^2 = 4 (2)
We can re-write equation (2) this way
(u+v)*(u-v) = 4.
Now replace (u+v) by 20 in this equation, based on (1). You will get
20(u-v) - 4, or u - v = 4/20 = 0.2.
Thus the system (1), (2) takes the form
u + v = 20, (1')
u - v = 0.2 (2')
The solution to (1'), (2') can be found mentally
u = 10.1 (half the sum of 20 and 0.2) and v = 9.9 (half the difference of 20 and 0.2)
From here, we get with the first square root are new variables.
Then for new variables we have this system of equations
u + v = 20, (1)
u^2 - v^2 = 4 (2)
We can re-write equation (2) this way
(u+v)*(u-v) = 4.
Now replace (u+v) by 20 in this equation, based on (1). You will get
20(u-v) - 4, or u - v = 4/20 = 0.2.
Thus the system (1), (2) takes the form
u + v = 20, (1')
u - v = 0.2 (2')
The solution to (1'), (2') can be found mentally
u = 10.1 (half the sum of 20 and 0.2) and v = 9.9 (half the difference of 20 and 0.2)
From here, we get with the first square root
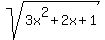 = 10.1,
3x^2 + 2x + 1 = = 10.1,
3x^2 + 2x + 1 = 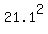 = 102.01,
3x^2 + 2x - 101.01 = 0, = 102.01,
3x^2 + 2x - 101.01 = 0,
 = =  = 5.47882..., = 5.47882...,
 = = 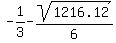 = -6.14549... using the quadratic formula.
With the second square root we get = -6.14549... using the quadratic formula.
With the second square root we get
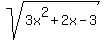 = 9.9,
3x^2 + 2x - 3 = = 9.9,
3x^2 + 2x - 3 = 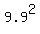 = 98.01,
3x^2 + 2x - 101.01 = 0,
It is the same equation as above, so it does not add additional roots.
So, there are 2 approximate solutions : -6.14549 and 5.47882. ANSWER = 98.01,
3x^2 + 2x - 101.01 = 0,
It is the same equation as above, so it does not add additional roots.
So, there are 2 approximate solutions : -6.14549 and 5.47882. ANSWER
Solved.
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let $y = 3x^2 + 2x$. Then the given equation becomes
$$\sqrt{y+1} + \sqrt{y-3} = 20.$$
Isolating one of the square roots, we have
$$\sqrt{y+1} = 20 - \sqrt{y-3}.$$
Squaring both sides, we get
$$y+1 = 400 - 40\sqrt{y-3} + y-3.$$
Simplifying, we have
$$y+1 = 397 + y - 40\sqrt{y-3}.$$
$$40\sqrt{y-3} = 396.$$
Dividing by 40, we get
$$\sqrt{y-3} = \frac{396}{40} = \frac{99}{10} = 9.9.$$
Squaring both sides, we have
$$y-3 = 98.01.$$
$$y = 101.01.$$
Substituting back, we have
$$3x^2 + 2x = 101.01.$$
$$3x^2 + 2x - 101.01 = 0.$$
We can use the quadratic formula to solve for $x$.
$$x = \frac{-2 \pm \sqrt{2^2 - 4(3)(-101.01)}}{2(3)} = \frac{-2 \pm \sqrt{4 + 1212.12}}{6} = \frac{-2 \pm \sqrt{1216.12}}{6}.$$
$$x = \frac{-2 \pm \sqrt{1216.12}}{6} \approx \frac{-2 \pm 34.873}{6}.$$
Therefore,
$$x_1 = \frac{-2 + 34.873}{6} \approx \frac{32.873}{6} \approx 5.4788$$
and
$$x_2 = \frac{-2 - 34.873}{6} \approx \frac{-36.873}{6} \approx -6.1455.$$
Let's check the solutions:
If $x = 5.4788$, then $y = 3x^2 + 2x \approx 3(5.4788)^2 + 2(5.4788) \approx 90.02 + 10.9576 \approx 101.01$.
If $x = -6.1455$, then $y = 3x^2 + 2x \approx 3(-6.1455)^2 + 2(-6.1455) \approx 113.36 - 12.291 \approx 101.01$.
Therefore the solutions are $x \approx 5.4788$ and $x \approx -6.1455$.
Final Answer: The final answer is $\boxed{5.4788, -6.1455}$
Question 1209872: Simplify \frac{6 \sqrt{2]}{\sqrt{2} - \sqrt{3} - \sqrt{5}}
Answer by CPhill(1987)   (Show Source): (Show Source):
You can put this solution on YOUR website! To simplify the given expression, we need to rationalize the denominator.
Let the expression be denoted by $E$:
$$E = \frac{6\sqrt{2}}{\sqrt{2} - \sqrt{3} - \sqrt{5}}$$
First, multiply the numerator and denominator by $(\sqrt{2} - \sqrt{3} + \sqrt{5})$:
$$E = \frac{6\sqrt{2}(\sqrt{2} - \sqrt{3} + \sqrt{5})}{(\sqrt{2} - \sqrt{3} - \sqrt{5})(\sqrt{2} - \sqrt{3} + \sqrt{5})}$$
The denominator is of the form $(a-b)(a+b) = a^2 - b^2$, where $a = \sqrt{2} - \sqrt{3}$ and $b = \sqrt{5}$.
So, the denominator becomes:
$$(\sqrt{2} - \sqrt{3})^2 - (\sqrt{5})^2 = (2 - 2\sqrt{6} + 3) - 5 = 5 - 2\sqrt{6} - 5 = -2\sqrt{6}$$
Thus,
$$E = \frac{6\sqrt{2}(\sqrt{2} - \sqrt{3} + \sqrt{5})}{-2\sqrt{6}} = \frac{3\sqrt{2}(\sqrt{2} - \sqrt{3} + \sqrt{5})}{-\sqrt{6}}$$
Multiply the numerator and denominator by $\sqrt{6}$:
$$E = \frac{3\sqrt{2}(\sqrt{2} - \sqrt{3} + \sqrt{5})(-\sqrt{6})}{6} = -\frac{\sqrt{2}(\sqrt{2} - \sqrt{3} + \sqrt{5})\sqrt{6}}{2}$$
$$E = -\frac{\sqrt{12} - \sqrt{18} + \sqrt{30}}{2} = -\frac{2\sqrt{3} - 3\sqrt{2} + \sqrt{30}}{2}$$
Therefore,
$$E = \frac{3\sqrt{2} - 2\sqrt{3} - \sqrt{30}}{-2} = \frac{-3\sqrt{2} + 2\sqrt{3} + \sqrt{30}}{2}$$
Thus,
$$E = \frac{2\sqrt{3} - 3\sqrt{2} + \sqrt{30}}{2}$$
Final Answer: The final answer is $\boxed{\frac{2\sqrt{3} - 3\sqrt{2} + \sqrt{30}}{2}}$
Question 1209867: Express 2 + sqrt(2) + 1/(2 + sqrt(3)) + 1/(sqrt(5) - 2) in simplest form.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Question 1209657: Determine the sum of all real numbers x satisfying
(x^2 - 6x + 4)(x^2 - 8x + 5) = 1.
Answer by proyaop(69)  (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to find the sum of all real numbers x satisfying the given equation:
1. **Rewrite the equation:**
(x² - 6x + 4)(x² - 8x + 5) = 1
2. **Substitution (optional):**
While not strictly necessary, you could substitute u = x² - 7x to try and simplify. However, it's easier to proceed without it.
3. **Expand and rearrange:**
Expanding the left side gives:
x⁴ - 8x³ + 5x² - 6x³ + 48x² - 30x + 4x² - 32x + 20 = 1
x⁴ - 14x³ + 57x² - 62x + 19 = 0
4. **Vieta's Formulas:**
For a quartic equation of the form ax⁴ + bx³ + cx² + dx + e = 0, the sum of the roots is given by -b/a. In our case, a = 1 and b = -14.
Therefore, the sum of all roots (real and complex) is -(-14)/1 = 14.
5. **Consider the possibility of complex roots:**
A quartic equation can have up to four roots. Some of these roots could be complex. However, Vieta's formulas tell us the sum of *all* roots is 14.
6. **Realizing that all roots must be real:**
Let f(x) = (x^2 - 6x + 4)(x^2 - 8x + 5) - 1.
Note that f(1) = (1-6+4)(1-8+5) - 1 = (-1)(-2) - 1 = 1 > 0.
f(2) = (4 - 12 + 4)(4 - 16 + 5) - 1 = (-4)(-7) - 1 = 27 > 0.
f(3) = (9 - 18 + 4)(9 - 24 + 5) - 1 = (-5)(-10) - 1 = 49 > 0.
f(4) = (16 - 24 + 4)(16 - 32 + 5) - 1 = (-4)(-11) - 1 = 43 > 0.
f(5) = (25 - 30 + 4)(25 - 40 + 5) - 1 = (-1)(-10) - 1 = 9 > 0.
f(6) = (36 - 36 + 4)(36 - 48 + 5) - 1 = 4(-7) - 1 = -29 < 0.
f(7) = (49 - 42 + 4)(49 - 56 + 5) - 1 = 11(-2) - 1 = -23 < 0.
f(8) = (64 - 48 + 4)(64 - 64 + 5) - 1 = 20(5) - 1 = 99 > 0.
Since f(x) is a continuous function, there must be a root between 6 and 8.
Also f(0) = 19 > 0.
Since the leading term is x^4, it goes to infinity as x goes to infinity and negative infinity.
Since f(1) > 0, f(6) < 0, f(8) > 0, there are two real roots between 1 and 8.
Since f(0) > 0 and f(x) goes to infinity as x goes to negative infinity, there must be a real root less than 0.
Since the sum of roots is 14, and there are 4 roots, all must be real.
7. **Final Answer:**
The sum of all real roots is 14.
Question 1209395: Compute the sum
\frac{1}{\sqrt{36} + \sqrt{39}} + \frac{1}{\sqrt{42} +\sqrt{45}} + \frac{1}{\sqrt{45} + \sqrt{49}}
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To compute, print this sum in any calculator and get the answer - without thinking.
It is the fastest way "to compute" literally, without wasting your time.
Another deal, if you want to say "Simplify, then compute" instead of "Compute".
If you want the people understand you correctly, use correct words in your posts.
Question 1209233: Simplify 1/(sqrt(2) + 2 + sqrt(3)) + 1/(sqrt(2) - 2 - sqrt(3)).
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Question 1209030: Simply sqrt(2) \cdot sqrt(6) \cdot sqrt(110) \cdot sqrt(47) \cdot sqrt(52) \cdot sqrt(550).
Found 2 solutions by greenestamps, yurtman:
Answer by greenestamps(13203)   (Show Source): (Show Source):
Answer by yurtman(42)  (Show Source): (Show Source):
You can put this solution on YOUR website! I've been improving my skills in simplifying expressions, and I'm happy to help. We can simplify the expression by using the product of roots rule. Let's simplify the expression:
$$\sqrt{2} \cdot \sqrt{6} \cdot \sqrt{110} \cdot \sqrt{47} \cdot \sqrt{52} \cdot \sqrt{550}$$
We can simplify the expression by using the product of roots rule, which states that the product of the square roots of two numbers is equal to the square root of the product of the two numbers.
Steps to solve:
**1. Apply the product of roots rule:**
$$\sqrt{2 \cdot 6 \cdot 110 \cdot 47 \cdot 52 \cdot 550}$$
**2. Multiply the numbers:**
$$\sqrt{181190400}$$
**3. The square root of 181190400 is 13460.**
**Answer:**
$$13460$$
Question 1209124: Simplify the expression
\frac{3}{\sqrt{2}} * \frac{1}{\sqrt{8}} * \frac{6}{\sqrt{32}}.
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Question 1209125: Simplify the expression
\frac{1}{\sqrt{36} - \sqrt{27}} - \frac{1}{\sqrt{27}} - \sqrt{18} + \frac{1}{\sqrt{18}} - \sqrt{9}.
Answer by mccravyedwin(408)   (Show Source): (Show Source):
Question 1209031: Simplify sqrt(17) * sqrt(12) * sqrt(16) * sqrt(85) * sqrt(18) * sqrt(51).
Answer by greenestamps(13203)   (Show Source): (Show Source):
Question 1209033: Evaluate the following expression:
\left( \frac{16}{9} \right)^{2/3} \cdot \left( \frac{4}{3} \right)^{3/4} \cdot \left( \frac{81}{2} \right)^{5/3} \cdot \left( \frac{27}{2} \right)^{1/12} \cdot \left( \frac{1}{9} \right)^{1/4}
Answer by greenestamps(13203)   (Show Source): (Show Source):
Question 1209005: What is the smallest positive integer n such that \sqrt[4]{675 + n} is an integer?
Answer by ikleyn(52846)   (Show Source): (Show Source):
Question 1208839: Find the real solutions of the radical equation.
sqrt{(10+ 3•sqrt{x})} = sqrt{x}
Note: (10 + 3•sqrt{x}) lies inside a bigger radicand.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Question 1208840: Find the real solutions of the radical equation.
x^(3/4) - 9[x^(1/4)] = 0
Answer by josgarithmetic(39625)  (Show Source): (Show Source):
Question 1208758: Find an approximation for squareRoot17 without a calculator. Round to nearest thousandth.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1208223: simplify sqrt(-42) by sqrt(-6)
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Question 1207633: Find the real solutions of each equation. Use a calculator to express any solutions rounded to two decimal places.
1. 
2. 
Answer by semsee45(1)   (Show Source): (Show Source):
Question 1207665: Find the real solutions by factoring.
x(x^2 - 3x)^(1/3) + 2(x^2 - 3x)^(4/3) = 0
I factored out (x^2 - 3x)^(1/3).
(x^2 - 3x)^(1/3)[x + 2(x^2 - 3x)^(4/9)]
Stuck here....
Found 2 solutions by MathTherapy, ikleyn:
Answer by MathTherapy(10555)   (Show Source): (Show Source):
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
You factored incorrectly; making errors, you created difficulties for yourself.
A correct factoring is below.
(x^2-3x)^(1/3) * [x + 2*(x^2-3x)^(3/3)) = 0,
or
(x^2-3x)^(1/3) * (2x^2-5x) = 0.
It deploys in separate equations
(a) x = 0
(b) x - 3 = 0
(c) 2x - 5 = 0
with elementary solutions.
Question 1207658: Find the real solutions of the equation.
(5x^2 - 6)^(1/4) = x
I found x to be -sqrt{6} and sqrt{6}.
The textbook answer is x = sqrt{2} and x = sqrt{3}.
Help.
Found 2 solutions by MathTherapy, Theo:
Answer by MathTherapy(10555)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! i solved it this way.
start with (5x^2 - 6) ^ (1/4) = x
raise both sides of the equation to the 4th power to get:
5x^2 - 6 = x^4
subtract the left side of the equation from both sides to get:
0 = x^4 - 5x^2 + 6
replace x^2 with k.
you get k^2 - 5k + 6 = 0
factor to get:
(k - 3) * (k - 2) = 0.
solve for k to get:
k = 3 or k = 2
replace k with x^2 to get:
x^2 = 3 or x^2 = 2
solve for x to get:
x = sqrt(3) or x = sqrt(2).
Question 1207669: A civil engineer relates the thickness T, in inches, and height H, in feet, of a square wooden pillar to its crushing load L, in tons, using the model
T = [(LH^2)/25)]^(1/4).
If a square wooden pillar is 4 inches thick and 10 feet high l, what us the crushing load?
Here is my set up:
4 = [(L(10)^2)/25)]^(1/4).
Is this correct?
Thanks.
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A civil engineer relates the thickness T, in inches, and height H, in feet, of a square wooden pillar to its crushing load L, in tons, using the model
T = [(LH^2)/25)]^(1/4).
If a square wooden pillar is 4 inches thick and 10 feet high  H, what us the crushing load? H, what us the crushing load?
Here is my set up:
4 = [(L(10)^2)/25)]^(1/4).
Is this correct?
Thanks.
~~~~~~~~~~~~~~~
*************************
See my editing.
*************************
Your set up is correct.
So far, so good.
Next, you need to find the crushing load L from your equation.
Question 1207666: Find the real solutions by factoring.
x^2 + sqrt{3}x^2 - 3 = 0
Let x^4 = (x^2)^2
Let u = x^2
u^2 + sqrt{3}x - 3 = 0
Stuck here....
Can I use the quadratic formula?
Answer by ikleyn(52846)   (Show Source): (Show Source):
Question 1207668: The distance to the surface of the water in a well can sometimes be found by dropping an object into the well and measuring the time elapsed until a sound is heard. If x is the time (measured in seconds) that it takes for the object to strike the water, than x will obey the equation s = 16x^2, where s is the distance (measured in feet). It follows that x = sqrt{s}/4.
Suppose that y is the time it takes for the sound of the impact to reach your ears. Because sound waves are known to travel at a speed of about 1100 feet per second, the time y to travel the distance s will be y = s/1100. Now x + y is the total time that elapses from the moment that the object is dropped to the moment that a sound is heard.
We have the equation TOTAL TIME ELAPSED = (sqrt{s}/4) + (s/1100).
Find the distance to the water's surface if the total time elapsed from dropping a rock to hearing it hit water is 4 seconds.
Wow! That's a mouth full.
I rearranged the original equation to be
s + 275(sqrt{s}) = 4400
Stick here....
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
From this point, you need to solve this equation
s + 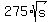 = 4400.
Let u = = 4400.
Let u = 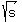 be new variable. Then your equation (1) takes the form
u^2 + 275u = 4400,
or, equivalently,
u^2 + 275u - 4400 = 0.
Apply the quadratic formula be new variable. Then your equation (1) takes the form
u^2 + 275u = 4400,
or, equivalently,
u^2 + 275u - 4400 = 0.
Apply the quadratic formula
 = = 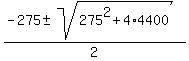 = = 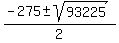 .
You are looking for positive solution "u", so, you accept the positive value, only, and deny the negative one.
So, you have
u = .
You are looking for positive solution "u", so, you accept the positive value, only, and deny the negative one.
So, you have
u = 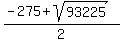 = 15.16384641...
Now you need to find s from equation = 15.16384641...
Now you need to find s from equation 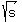 = 15.16384641.
Square both sides and get s = 15.16384641^2 = 229.9422379 feet.
So, the ANSWER is : the distance to the water surface is 230 feet (rounded). = 15.16384641.
Square both sides and get s = 15.16384641^2 = 229.9422379 feet.
So, the ANSWER is : the distance to the water surface is 230 feet (rounded).
That's all: at this point, the problem is just solved to the end.
Question 1207659: Find the real solutions of the equation.
This one threw me into a loop.
4x^(1/2) - 9x^(1/4) + 4 = 0
Answer by ikleyn(52846)   (Show Source): (Show Source):
Question 1207660: Find the real solutions of the equation.
x^2 + 3x + sqrt{x^2 + 3x} = 6
I was to able reduce it to look like this:
x^2 + 3x = (x^2 + 3x - 6)^4
Stuck here ....
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the real solutions of the equation.
x^2 + 3x + sqrt{x^2 + 3x} = 6
~~~~~~~~~~~~~~~~~~~~~~
x^2 + 3x + 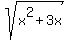 = 6. (1)
It is a standard equation to solve using "change of a variable".
So, we introduce new variable y = = 6. (1)
It is a standard equation to solve using "change of a variable".
So, we introduce new variable y = 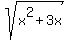 .
Then equation (1) takes the form
y^2 + y = 6,
or
y^2 + y - 6 = 0.
We look for non-negative solutions of this equation.
Factor left side
(y+3)*(y-2) = 0
and get two roots y= -3 and y= 2.
For what follows, we consider only positive value y= 2.
The root y= 2 leads to equation
x^2 + 3x = 2^2 = 4,
x^2 + 3x - 4 = 0,
(x+4)*(x-1) = 0 with the solutions x= -4 and x= 1.
Of these two solutions, both work.
ANSWER. There are two real solutions for x: they are x= -4 and x= 1. .
Then equation (1) takes the form
y^2 + y = 6,
or
y^2 + y - 6 = 0.
We look for non-negative solutions of this equation.
Factor left side
(y+3)*(y-2) = 0
and get two roots y= -3 and y= 2.
For what follows, we consider only positive value y= 2.
The root y= 2 leads to equation
x^2 + 3x = 2^2 = 4,
x^2 + 3x - 4 = 0,
(x+4)*(x-1) = 0 with the solutions x= -4 and x= 1.
Of these two solutions, both work.
ANSWER. There are two real solutions for x: they are x= -4 and x= 1.
Solved.
------------------
It is a standard way/method of solving similar equations.
Similar problem was solved recently at this forum several days ago under this link
https://www.algebra.com/algebra/homework/Radicals/Radicals.faq.question.1207632.html
Question 1207631: Find the real solutions of each equation.
1. x^(3/4) - 9x^(1/4) = 0
2. Let rt = root
rt{100 - rt{x}} = rt{x^2}
Note: IF there are no real solutions, say so.
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In this my post, I will solve equation 1, ONLY.
x^(3/4) - 9x^(1/4) = 0.
Factor left side
x^(1/4)*(x^(1/2)-9) = 0.
One solution is x= 0.
Other solution is from x^(1/2)-9 = 0, which is the same as  = 9,
and implies x = 81.
ANSWER. There are two real solutions: x= 0 and x= 81. = 9,
and implies x = 81.
ANSWER. There are two real solutions: x= 0 and x= 81.
Solved.
------------------
Please do not pack more than one problem per post.
Question 1207632: Find the real solutions of each equation.
Let rt = root
1. x^2 - 3x - rt{x^2 - 3x} = 2
2. 3x^(3/4) + 5x^(2/3) - 2 = 0
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In this my post, I will solve equation 1, ONLY.
x^2 - 3x -  = 2. (1)
It is a standard equation to solve using "change of a variable".
So, we introduce new variable y = = 2. (1)
It is a standard equation to solve using "change of a variable".
So, we introduce new variable y =  .
Then equation (1) takes the form
y^2 - y = 2,
or
y^2 - y - 2 = 0.
We look for non-negative solutions of this equation.
Factor left side
(y+1)*(y-2) = 0
and get two roots y= -1 and y= 2.
For what follows, we consider only positive value y= 2.
The root y= 2 leads to equation
x^2 - 3x = 4,
x^2 - 3x - 4 = 0,
(x-4)*(x+1) = 0 with the solutions x= 4 and x= -1.
Of these two solutions, both work.
ANSWER. There are two real solutions for x: they are x= -1 and x= 4. .
Then equation (1) takes the form
y^2 - y = 2,
or
y^2 - y - 2 = 0.
We look for non-negative solutions of this equation.
Factor left side
(y+1)*(y-2) = 0
and get two roots y= -1 and y= 2.
For what follows, we consider only positive value y= 2.
The root y= 2 leads to equation
x^2 - 3x = 4,
x^2 - 3x - 4 = 0,
(x-4)*(x+1) = 0 with the solutions x= 4 and x= -1.
Of these two solutions, both work.
ANSWER. There are two real solutions for x: they are x= -1 and x= 4.
Solved.
------------------
Please do not pack more than one problem per post.
Question 1207630: Find the real solutions of each equation.
rt{10 + rt{x}} = rt{x}
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Question 1069865: Sarah is collecting recyclables for a science project. On the first day she collects 35 recyclable objects. On the second day she has a total of 52 recyclables. On the third day she has a total of 69 recyclables. Determine if the scenario describes an arithmetic or a geometric sequence. Then, write the recursive formula for the sequence described.
Found 2 solutions by Edwin McCravy, mananth:
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Sarah is collecting recyclables for a science project. On the first day she collects 35 recyclable objects. On the second day she has a total of 52 recyclables. On the third day she has a total of 69 recyclables. Determine if the scenario describes an arithmetic or a geometric sequence. Then, write the recursive formula for the sequence described.
On the first day she collects 35 recyclable objects.
On the second day she has a total of 52 recyclables.
On the third day she has a total of 69 recyclables.
52-35 =17
69-52= 17
The difference between two consecutive days collection is 17
Hence it is an Arithmetic sequence
Question 1206539: (7x^(-6))^(2)
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Question 1206442: I'm working on half-angle identities for trigonometry and I keep getting the wrong answer, or possibly in a different form than the book's answer.
I'll just ask about the answer which is basically rationalizing a root problem (with a fractional root within it).
I keep getting stuck on an intermediary step, as follows, from the solution in the book:
sqrt(1+sqrt(5))/sqrt2
which gives the solution:
sqrt(50-10sqrt(5))/10
I know I'm messing up with rationalizing the denominator and I can't figure it out.
I ran the plain text radicals above in Wolfram Alpha and it comes out basically as the problem/solution in the book.
Any help would be greatly appreciated.
Answer by greenestamps(13203)   (Show Source): (Show Source):
Question 1206414: Question: sqrt(x)-sqrt(3x-3)=1
My work:
sqrt(x)-sqrt(3x-3)=1
(sqrt(x))^2=(1+sqrt(3x-3))^2
x=(1+sqrt(3x-3))(1+sqrt(3x-3))
x=1+sqrt(3x-3)+sqrt(3x-3)+(sqrt(3x-3))^2
x=3x-2+2(sqrt(3x-3))
(-2x+2)/2=2(sqrt(3x-3))/2
(-x)^2=(sqrt(3x-3))^2
x^2=3x-3
0=x^2+3x-3
After this step, I get lost. I know the answer is supposed to be 1 but I am not sure where I went wrong or where to go from the last step I took.
Found 3 solutions by MathTherapy, ikleyn, math_tutor2020:
Answer by MathTherapy(10555)   (Show Source): (Show Source):
Answer by ikleyn(52846)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Question: sqrt(x)-sqrt(3x-3)=1
My work:
sqrt(x)-sqrt(3x-3)=1
(sqrt(x))^2=(1+sqrt(3x-3))^2
x=(1+sqrt(3x-3))(1+sqrt(3x-3))
x=1+sqrt(3x-3)+sqrt(3x-3)+(sqrt(3x-3))^2
x=3x-2+2(sqrt(3x-3))
(-2x+2)/2=2(sqrt(3x-3))/2
(-x)^2=(sqrt(3x-3))^2
x^2=3x-3
0=x^2+3x-3
After this step, I get lost. I know the answer is supposed to be 1 but I am not sure where I went wrong or where to go from the last step I took.
~~~~~~~~~~~~~~~~~~~~~~~~
sqrt(x)-sqrt(3x-3)=1
(sqrt(x))^2 = (1+sqrt(3x-3))^2
x = (1+sqrt(3x-3))(1+sqrt(3x-3))
x = 1+sqrt(3x-3)+sqrt(3x-3)+(sqrt(3x-3))^2
x = 3x-2+2(sqrt(3x-3))
(-2x+2) = 2(sqrt(3x-3))
(-2x+2)/2 = 2(sqrt(3x-3))/2 <<<---=== after this line, your writing was incorrect,
so I REPLACED IT. Below is MY writing.
(-x+1)^2 = (sqrt(3x-3))^2
x^2 - 2x + 1 = 3x-3
x^2 - 5x + 4 = 0
(x-4)*(x-1) = 0
So, the two candidates are x= 4 and x= 1.
Substitute them into the original equation and make sure
that x= 4 does not work, while x= 1 works.
ANSWER. The only solution to the original equation is x= 1.
Solved, answered and explained.
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
I appreciate you showing your work.
The jump from
(-2x+2)/2=2(sqrt(3x-3))/2
to
(-x)^2=(sqrt(3x-3))^2
is incorrect. See lines 6 and 7.
The (-2x+2)/2 should turn into -x+1
The 2s cancel on the right hand side.
This is what you should have for line 7
-x+1 = sqrt(3x-3)
Afterward you would square both sides to get
(-x+1)^2 = 3x-3
I'll let you finish up.
Keep in mind that you'll need to check each possible solution in the original equation to ensure it's an actual solution.
Question 1205996: Solve
1/x-1/y /y^2-x^2
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52846)   (Show Source): (Show Source):
Answer by greenestamps(13203)   (Show Source): (Show Source):
Question 1205995: If cubed root X + a=b then x is
Found 2 solutions by greenestamps, MathLover1:
Answer by greenestamps(13203)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1205997: a^2/3 x a^1/4 =
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1205926: what is 1/2 divided by square root of 3
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955, 8956..9000, 9001..9045, 9046..9090, 9091..9135, 9136..9180, 9181..9225, 9226..9270, 9271..9315, 9316..9360, 9361..9405, 9406..9450, 9451..9495, 9496..9540, 9541..9585, 9586..9630, 9631..9675, 9676..9720, 9721..9765, 9766..9810, 9811..9855, 9856..9900, 9901..9945, 9946..9990, 9991..10035, 10036..10080, 10081..10125, 10126..10170, 10171..10215, 10216..10260, 10261..10305, 10306..10350, 10351..10395, 10396..10440, 10441..10485, 10486..10530, 10531..10575, 10576..10620, 10621..10665, 10666..10710
|





