Question 159089: A farmer with 10,000 meters of fencing wants to enclose a rectangular field and then divide it into three plots with two fences parallel to one of the sides. What is the area that can be enclosed? I need to find the vertex but cannot figure out how to solve this problem. (Analyzing Graphs of Quadratic Functions).
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A farmer with 10,000 meters of fencing wants to enclose a rectangular field and
then divide it into three plots with two fences parallel to one of the sides.
What is the area that can be enclosed? I need to find the vertex
:
They want to find the max area that can be enclosed which is the vertex
:
Since they want three plots, we will have two lengths and four widths
:
Let L = length, Let x = the width
;
2L + 4x = 10000
Simplify divide by 2
L + 2x = 5000
:
L = (5000 - 2x)
;
Area = L*x
Substitute (5000-2x) for L
A = (5000-2x) * x
:
A quadratic equation
A = -2x^2 + 5000x
:
When you want to find the vertex, you don't want to simplify the equation
:
To find the vertex, find the axis of symmetry; x = -b/(2a): a=-2, b=5000
:
x = 
x = 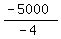
x = +1250 meters is the width for max area
:
Find the max area, substitute 1250 for x in the area equation:
A = -2(1250^2) + 5000(1250)
A = -3125000 + 6250000
A = 3,125,000 sq meters is the max area
:
The vertex: 1250, 3,125,000
:
:
Did this make sense to you? Any questions?
|
|
|