Question 118649: A theatre seats 500 people per show and is currently sold out with a ticket price of $16. A survey shows that for every $2 per ticket price increase, 25 fewer tickets will be sold.Write a function to model this situation and use this function to determine the ticket price that will result in the greatest revenue per show.
I tried (25x-500)(2x-16)=0
50x^2-400x-1000x+8000
x^2-28+150
x=-b/a=28/2=$14
BUT lost several marks :( Can anyone tell me why :)
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website! A theatre seats 500 people per show and is currently sold out with a ticket price of $16. A survey shows that for every $2 per ticket price increase, 25 fewer tickets will be sold.Write a function to model this situation and use this function to determine the ticket price that will result in the greatest revenue per show.
I tried (25x-500)(2x-16)=0
50x^2-400x-1000x+8000
x^2-28+150
x=-b/a=28/2=$14
BUT lost several marks :( Can anyone tell me why :)
One of the best ways to explain a word problem is by
first looking at an example using an arbitrary number,
like, say, 7. For the reasoning involved in setting
up an equation is the same.
Suppose there are 7 $2 increases.
Then the ticket price is figured by multiplying $2 by 7,
getting $14, and adding to the original price of $16,
getting $14 + 16$ or $30.
Then the number of tickets sold is gotten by multiplying
7 by 25, getting 175 and subtracting from 500, getting
500 - 175, or 325.
Then to get the revenue, we multiply $30 by 325 and get
$9750.
So the equation for the revenue, R(7) is
R(7) = $9750
----------------------
Now let's use that same reasoning, and the same
words, only this time using x instead of 7.
Suppose there are x $2 increases.
Then the ticket price is figured by
multiplying $2 by x, getting $2x, and adding to the
original price of $16, getting $16 + $2x or $2(8 + x).
Then the number of tickets sold is gotten by multiplying
x by 25, getting 25x and subtracting from 500, getting
500 - 25x, or 25(20-x).
Then to get the revenue, we multiply $2(8 + x) by 25(20 - x)
and get $50(8 + x)(20 - x)
So the equation for the revenue, R(x) is
R(x) = $50(8 + x)(20 - x)
Now to get the maximum revenue, we multply
that out
R(x) = 50(160+12x-x²)
R(x) = 8000 + 600x - 50x²
or, in descending order
R(x) = -50x² + 600x + 8000
Now we'll replace R(x) by y and
get the equation
y = -50x² + 600x + 8000
The graph of that equation is this parabola:
 To get the highest point on that graph, called the
"vertex", we use the vertex formula:
For the graph of the parabola y = ax² + bx + c,
the vertex is the point (
To get the highest point on that graph, called the
"vertex", we use the vertex formula:
For the graph of the parabola y = ax² + bx + c,
the vertex is the point ( , ,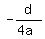 )
where d = b² - 4ac, the discriminant.
For the graph of the parabola y = -50x² + 600x + 8000,
we calculate d = (600)² - 4(-50)(8000) = 1960000
So the vertex is the point ( )
where d = b² - 4ac, the discriminant.
For the graph of the parabola y = -50x² + 600x + 8000,
we calculate d = (600)² - 4(-50)(8000) = 1960000
So the vertex is the point (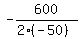 , ,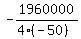 )
or ( )
or (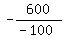 , ,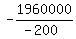 )
or (6,9800)
which means if there are 6 increases of $2, the most possible
revenue of $9800 will be received. 6 increases of $2 amounts
to increasing the original price of $16 per ticket by $12,
making the optimum price to charge per ticket $28.
Edwin )
or (6,9800)
which means if there are 6 increases of $2, the most possible
revenue of $9800 will be received. 6 increases of $2 amounts
to increasing the original price of $16 per ticket by $12,
making the optimum price to charge per ticket $28.
Edwin
|
|
|