|
Question 887025: find the equation of ellipse with eccentricity 2 and distance between foci 4 square root of 2
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! Your question is missing information (and understanding).
For an ellipse, or a hyperbola, there are three related length measurements symbolized by  , ,  , and , and  . .
You need two of those and some other information to be able to write the equation.
 = focal distance (distance from center to one of the foci), = focal distance (distance from center to one of the foci),
so that 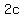 = distance between foci. = distance between foci.
In your case,  ---> ---> ---> --->
 = semi-major axis (from the center to one of the vertices). = semi-major axis (from the center to one of the vertices).
 is between 0 and 1 for an ellipse, and greater then 1 for a hyperbola. is between 0 and 1 for an ellipse, and greater then 1 for a hyperbola.
In your case,  , so you seem to have a hyperbola , so you seem to have a hyperbola
 ---> ---> ---> ---> ---> ---> ---> ---> <---> <--->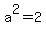
There is also  , sometimes called semi-minor axis for an ellipse. , sometimes called semi-minor axis for an ellipse.
For an ellipse,  , but for a hyperbola , but for a hyperbola  . .
In your case,




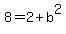


Knowing  , ,  , ,
the coordinates (h,k) of the center,
and the orientation of the ellipse or hyperbola (knowing the line that contains the major axis),
we can write the equation of the ellipse or hyperbola .
For example, an ellipse centered at (0,0) (the origin) with the x-axis as its major axis, like this 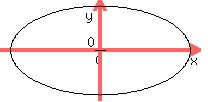
has the equation  . .
A hyperbola centered at (0,0) (the origin) with the x-axis as its major axis
looks sort of like this )( and
has the equation  . .
An ellipse centered at (0,0) (the origin) with the y-axis as its major axis
looks like this  has the equation has the equation
 . .
A hyperbola centered at (0,0) (the origin) with the y-axis as its major axis
looks like this 
has the equation  . .
If the center is at (h,k), the equation would be
 if the major axis is parallel to the x-axis, or if the major axis is parallel to the x-axis, or
 if the major axis is parallel to the x-axis. if the major axis is parallel to the x-axis.
(If the major axis was not parallel to the x- or y-axes, the equation would br really complicated, but you would be in an advance math course and would have asked the question in a different way).
|
|
|
| |