Question 874025: Q.there are exactly 2 points on the ellipse  whose distance from the center of the ellipse are equal to whose distance from the center of the ellipse are equal to 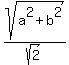 find the eccentricity of the ellipse. find the eccentricity of the ellipse.
here's what i tried:
Ans)since the ellipse is symmetric about x and y axis if there are only 2 points which satisfy a condition, they must lie on the x and y axis. which means that the two points are extremities of the ellipse on y-axis. thus on solving given distance = 2b we get e=sqrt(6/7) which is not the right answer
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There is a typo somewhere.
If an ellipse is given by the equation  , with , with  and and 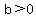 , ,
and there is at least one point whose distance from the center of the ellipse is equal to
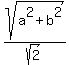 , ,
the ellipse is a circle, with radius  , ,
and all the infinite number of points on the ellipse are at a distance of
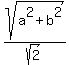 from the center of that ellipse, which is a circle. from the center of that ellipse, which is a circle.
The points on an ellipse whose distance from the center of the ellipse are equal to a given distance are all the points of a circle,
with that distance as the radio, and centered at the center of the ellipse.
It could be that circle and ellipse share no points :
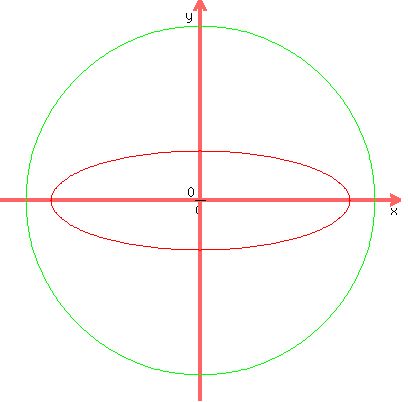 or or  . .
It could be that circle and ellipse share exactly two points :
 or or  . .
It could be that circle and ellipse share exactly four points :
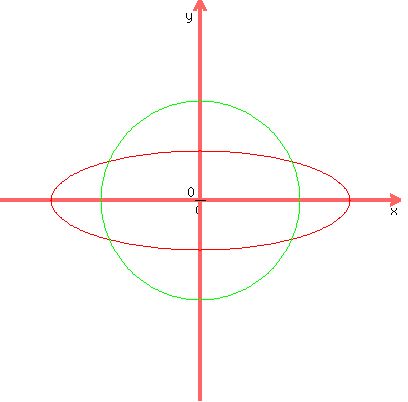 , ,
or it could be that the ellipse IS the same curve as the circle, and so they share all their infinite number of points.
The ellipse  , with , with  and and 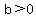 , is centered on the origin, , is centered on the origin,
so we are dealing with an ellipse and a circle centered (both of them) at (0,0), the origin.
The points the problem talks about are on the ellipse and on that circle.
If those points are exactly 2 points, they are either the vertices or the co-vertices.
That means, those points must be either (a,0) and {-a,0),
which are at a distance  from the origin, from the origin,
or those points must be either (0,b), and (0,-b),
which are at a distance  from the origin. from the origin.
If the distance is 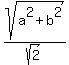 , as you posted, , as you posted,
then  or or  . .
However,
 --> --> --> --> --> --> --> --> --> --> , ,
and
 --> --> --> --> --> --> --> --> --> --> . .
Either way, the ellipse turns to be a circle of radius  , ,
and all of its infinite number of points are at a distance
 . .
NOTE - CHECK THE PROBLEM'S EQUATIONS:
If the distance were
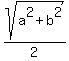 , then , then
 --> --> --> --> --> --> --> --> , ,
and if
 --> --> --> --> --> --> --> --> . .
In either case, the eccentricity would be the same.
If  <--> <--> , then , then 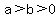 ; ;
 is the semi-major axis; is the semi-major axis;
the vertices are (a,0) and {-a,0);
 --> c+sqrt(4b^2)=2b}}} , --> c+sqrt(4b^2)=2b}}} ,
and the eccentricity is  . .
If  <--> <--> , then , then 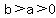 ; ;
 is the semi-major axis; is the semi-major axis;
the vertices are (0,b) and {0,-b);
 --> -->  , ,
and the eccentricity is 
|
|
|