|
Question 608616: Classify the conic section, write it's equation in standard form, and graph.
X^2+y^2+4x-6y-3=0
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi
Classify the conic section, write it's equation in standard form, and graph.
x^2+y^2+4x-6y-3=0
(x+2)^2-4 +(y-3)^2-9-3=0
(x+2)^2 +(y-3)^2 = 16 |Circle with C(-2,3) and r = 4
Note:
Standard Form of an Equation of a Circle is 
where Pt(h,k) is the center and r is the radius
See below descriptions of various conics
_______________________________________________________________________
Standard Form of an Equation of a Circle is
where Pt(h,k) is the center and r is the radius
Standard Form of an Equation of an Ellipse is  where Pt(h,k) is the center. (a positioned to correspond with major axis)
a and b are the respective vertices distances from center and ±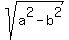 are the foci distances from center: a > b
Standard Form of an Equation of an Hyperbola opening right and left is:
 where Pt(h,k) is a center with vertices 'a' units right and left of center.
Standard Form of an Equation of an Hyperbola opening up and down is:
 where Pt(h,k) is a center with vertices 'b' units up and down from center.
the vertex form of a parabola opening up or down,  where(h,k) is the vertex.
The standard form is  , where the focus is (h,k + p)
the vertex form of a parabola opening right or left,  where(h,k) is the vertex.
The standard form is  , where the focus is (h +p,k )
|
|
|
| |
