SOLUTION: Find Standard Equation Of a Hyperbola: Given, Foci: (-8,0) and (8,0) Vertices: (-6,0) and (6,0).

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Find Standard Equation Of a Hyperbola: Given, Foci: (-8,0) and (8,0) Vertices: (-6,0) and (6,0).       Log On


   

Question 170281: Find Standard Equation Of a Hyperbola: Given, Foci: (-8,0) and (8,0) Vertices: (-6,0) and (6,0).
Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!
Take note that ALL of the points given to you (both vertices and foci) all have a y-coordinate of 0. So this tells us that the hyperbola opens left and right like this:



Photobucket - Video and Image Hosting



Take note that the distance from the center to either focus is 8 units. So let's call this distance "c" (ie c=8)


Remember, the equation of any hyperbola opening left/right is

%28%28x-h%29%5E2%29%2F%28a%5E2%29-%28%28y-k%29%5E2%29%2F%28b%5E2%29=1

So we need to find the values of h, k, a, and b


Now let's find the midpoint of the line connecting the vertices. This midpoint is the center of the hyperbola

x mid: Average the x-coordinates of the vertices: %28-8%2B8%29%2F2+=+0%2F2+=+0
So the x-coordinate of the center is 0. This means that h = 0
-------------------
y mid: Average the y-coordinates of the vertices: %280%2B0%29%2F2+=+0%2F2+=+0

So the y-coordinate of the center is 0. This means that k = 0

So the center is (0,0) which means that h=0 and k=0

------------------

Now because the hyperbola opens left and right, this means that the vertices are (h+a,k) and (h-a,k). In other words, you add and subtract the value of "a" to the x-coordinate of the center to get the vertices.


Since the value of "h" and "k" is 0, this means that the vertices become (0+a,0) and (0-a,0) then simplify to (a,0) and (-a,0)

So this tells us that a=6 and -a=-6 which simply means that a=6

-------------------------------------------------------------------

Now it turns out that the value of "b" is closely connected to the values of "a" and "c". They are connected by the equation


a%5E2%2Bb%5E2=c%5E2


6%5E2%2Bb%5E2=8%5E2 Plug in a=6 and c=8


36%2Bb%5E2=64 Square 6 to get 36. Square 8 to get 64


b%5E2=64-36 Subtract 36 from both sides.


b%5E2=28 Subtract


b=sqrt%2828%29 Take the square root of both sides. Note: only the positive square root is considered (since a negative distance doesn't make sense)


b=2%2Asqrt%287%29 Simplify the square root.


==========================================================
Recap:

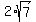So we found the following: h=0, k=0 (the x and y coordinates of the center), a=6 and b=2%2Asqrt%287%29



%28%28x-h%29%5E2%29%2F%28a%5E2%29-%28%28y-k%29%5E2%29%2F%28b%5E2%29=1 Start with the general equation for a hyperbola (one that opens left/right)


%28%28x-0%29%5E2%29%2F%286%5E2%29-%28%28y-0%29%5E2%29%2F%28%282%2Asqrt%287%29%29%5E2%29=1 Plug in h=0, k=0, a=6 and b=2%2Asqrt%287%29


%28%28x-0%29%5E2%29%2F%2836%29-%28%28y-0%29%5E2%29%2F%284%2A7%29=1 Square 6 to get 36. Square 2%2Asqrt%287%29 to get 4%2A7


%28%28x-0%29%5E2%29%2F%2836%29-%28%28y-0%29%5E2%29%2F%2828%29=1 Multiply


%28x%5E2%29%2F%2836%29-%28y%5E2%29%2F%2828%29=1 Simplify


==================================================================

Answer:


So the equation of the hyperbola that has the foci (8,0) and (-8,0) along with the vertices (-6,0) and (6,0) is:

%28x%5E2%29%2F%2836%29-%28y%5E2%29%2F%2828%29=1