|
Question 152896: The moon travels an elliptical path with Earth as one focus. The maximum distance from the moon to Earth is 405,500 km and the minimum distance is 363,300 km.
(1) What is the eccentricity of the orbit?
(2) For a planet or satellite in an elliptical orbit around a focus of the ellipse, perigee (P) is defined to be its closest distance to the focus and apogee (A) is defined to be its greatest distance from the focus. Show that 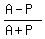 is equal to the eccentricity of the orbit. is equal to the eccentricity of the orbit.
(3) Find the Apogee. Find the Perigee.
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The moon travels an elliptical path with Earth as one focus. The maximum distance from the moon to Earth is 405,500 km and the minimum distance is 363,300 km.
(1) What is the eccentricity of the orbit?
Eccentricity = c/a
where c is the distance from the center to the focus of the ellipse
a is the distance from the center to a vertex
Here is a sketch:
 The ellipse represents the orbit of the moon.
So the coordinates of M are (4.055,0)
and the coordinates of N are (-3.633,0)
The ellipse has vertices are at M and N. The center of the ellipse,
R, is the midpoint between M and N, so we use the midpoint formula
midpoint = (
The ellipse represents the orbit of the moon.
So the coordinates of M are (4.055,0)
and the coordinates of N are (-3.633,0)
The ellipse has vertices are at M and N. The center of the ellipse,
R, is the midpoint between M and N, so we use the midpoint formula
midpoint = (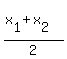 , , 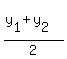 ),
midpoint = ( ),
midpoint = (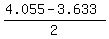 , ,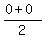 ) = (0.211,0)
and find that the center of the ellipse is R(0.211,0)
Since the focus of the ellipse is the earth at (0,0)
and the center of the ellipse is at R(0.211,0), the value of c
is c=0.211 units (distance from center to focus). That is c = 211 km.
the value of a is a= (the distance from the ellipse's center
(.211,0) to vertex M(4.055,0) is 4.055-.211 or 3.844 units, or a = 384400 km.
Therefore the eccentricity = ) = (0.211,0)
and find that the center of the ellipse is R(0.211,0)
Since the focus of the ellipse is the earth at (0,0)
and the center of the ellipse is at R(0.211,0), the value of c
is c=0.211 units (distance from center to focus). That is c = 211 km.
the value of a is a= (the distance from the ellipse's center
(.211,0) to vertex M(4.055,0) is 4.055-.211 or 3.844 units, or a = 384400 km.
Therefore the eccentricity =  -------------------------------------------------
(2) For a planet or satellite in an elliptical orbit around a focus
of the ellipse, perigee (P) is defined to be its closest distance to
the focus and apogee (A) is defined to be its greatest distance from
the focus. Show that
-------------------------------------------------
(2) For a planet or satellite in an elliptical orbit around a focus
of the ellipse, perigee (P) is defined to be its closest distance to
the focus and apogee (A) is defined to be its greatest distance from
the focus. Show that 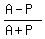 is equal to the eccentricity
of the orbit. is equal to the eccentricity
of the orbit.
 Now don't confuse the small
Now don't confuse the small  for the semi-major axis
with the capital for the semi-major axis
with the capital 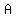 for the apogee. for the apogee.




 ------------------------------
(3) Find the Apogee and the Perigee of problem (1)
Apogee = 405,500 km
Perigee = 363,300 km
Checking the eccentricity using
------------------------------
(3) Find the Apogee and the Perigee of problem (1)
Apogee = 405,500 km
Perigee = 363,300 km
Checking the eccentricity using 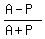 = =  Edwin
Edwin
|
|
|
| |