SOLUTION: The triangle with vertices (a,a), (a, 2a), (2a,2a) is rotated about: a) The x-axis b) The y- axis Find the volume in each case.

I will assume that "a" is positive real number.


Notice that this given triangle is SPECIAL. It has vertical leg from (a,a), to (a,2a) 
and horizontal leg from (a,2a) to (2a,2a).  


So, the triangle itself is a right angled triangle. It is "the upper half of the square"   a <= x, y <= 2a,
cut in two halves by its diagonal y = x.  It facilitates thinking and calculations.


          Let' consider rotation about x-axis.


The volume is the area of the ring in vertical section x= const, integrated over (or along) x-coordinate
from  x= a  to  x= 2a.  


The area of the ring is   = .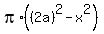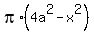


Thus the volume is the integral of the function 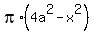   from  "a"  to  "2a".


The antiderivative is  the function  F(x) = .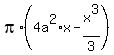


So, the final integral value is the difference  F(2a) - F(a), which is

     =  =  = .


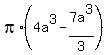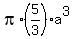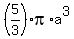Thus the volume of the body of revolution in this case is 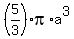 ,  in terms of "a", assuming "a" is positive.    ANSWER