SOLUTION: A cross section of a reflector of a television satellite dish is a parabola that measures 5 ft across with a depth of 2 ft. How far from the vertex should the receiving antenna be

Place the origin of the coordinate system at vertex of the parabola.
Use the vertex form equation of this parabola 

    y = .        (1)


At x = 2.5 ft, we are given y = 2 ft.  So, this vertex equation takes the form

    2 = 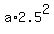,  which gives  a =  =  = .


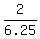So, equation (1) is  

    y = 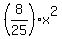.    (2)


For the parabola with equation y = ,  the distance from the vertex to the focus is

    f = .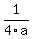


In our case, the distance from the vertex to the focus is 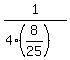   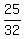=  cm = 0.78125 ft.


ANSWER.  The distance from the vertex to the focus, where the filament should be placed, is 0.78125 ft.  

         Option (B).