|
Question 1204362: A comet's path as it approaches the sun can be modeled by one branchof hyperbola y²/1225 - x²/40401 = 1, where the sun is at the focus of that path of the hyperbola. Each unit of the coordinate system is 1 million kilometers. Find the coordinates of the sun and how close the comet come to the sun.
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A comet's path as it approaches the sun can be modeled by one branchof hyperbola y²/1225 - x²/40401 = 1,
where the sun is at the focus of that path of the hyperbola. Each unit of the coordinate system
is 1 million kilometers. Find the coordinates of the sun and how close the comet come to the sun.
~~~~~~~~~~~~~~~~~~~~
One vertex of the hyperbola is the point V1 = (x,y) = (0,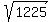 ) = (0,35).
The other vertex of the hyperbola is V2 = (x,y) = (0,- ) = (0,35).
The other vertex of the hyperbola is V2 = (x,y) = (0,-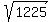 ) = (0,-35).
The real axis of the hyperbola (= the transverse axis) in this coordinate system is vertical segment [V1,V2].
The foci are the points F1 = (0, ) = (0,-35).
The real axis of the hyperbola (= the transverse axis) in this coordinate system is vertical segment [V1,V2].
The foci are the points F1 = (0,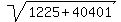 = (0,204.0245) and F2 = (0,-204.0245).
By identifying the position of the sun with the focus F1, we can say that the position of the sun is
F1 = (0,204.0245), or 204.0245 million kilometers along the y-axis.
Then the position of the comet, closest to the sun, is at vertex V1 = (0,35),
and the smallest distance the comet from the sun is 204.0245-35 = 169.0245 million kilometers.
ANSWER. Coordinates of the sun are x= 0, y= 204.0245 million kilometers.
The smallest distance of the comet from the sun is 169.0245 million kilometers. = (0,204.0245) and F2 = (0,-204.0245).
By identifying the position of the sun with the focus F1, we can say that the position of the sun is
F1 = (0,204.0245), or 204.0245 million kilometers along the y-axis.
Then the position of the comet, closest to the sun, is at vertex V1 = (0,35),
and the smallest distance the comet from the sun is 204.0245-35 = 169.0245 million kilometers.
ANSWER. Coordinates of the sun are x= 0, y= 204.0245 million kilometers.
The smallest distance of the comet from the sun is 169.0245 million kilometers.
Solved.
-------------------
For references, see this Internet site
https://courses.lumenlearning.com/waymakercollegealgebra/chapter/equations-of-hyperbolas/
|
|
|
| |