|
Question 1187463: Find the equation of the locus of a point which moves so that the sum of its distances from the points (2,1) and (8,1) is 10
Answer by ikleyn(52795)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the equation of the locus of a point which moves so
that the sum of its distances from the points (2,1) and (8,1) is 10
~~~~~~~~~~~~~~~~~
It is by the DEFINITION the locus of points such, that the sum of distances from two given points is constant, is an ELLIPSE.
So, the sough locus, or the sough set of points is an ellipse.
About this ellipse, we know that its major axis is horizontal y = 1.
We also know that the center of this ellipse is the point (5,1), where 5 is the arithmetic mean of 2 and 8,
which are x-coordinates of the foci.
We also know that the eccentricity of this ellipse is half the distance between the foci
c = 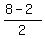 = = 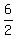 = 3.
Finally, we can calculate the length of the major semi-axis "a".
For it, we use the fact thant the sum of distances from the foci to any point of the ellipse is 10.
In particular, the sum (c+a) PLUS (a-c) from the foci to the right-most vertex of the ellipse is 10:
(c+a) + (a-c) = 10.
It gives 2a = 10; hence, a = 10/2 = 5.
By knowing "a" and "c" of the ellipse, we easily find "b", the length of the minor semi-axis: it is
b = = 3.
Finally, we can calculate the length of the major semi-axis "a".
For it, we use the fact thant the sum of distances from the foci to any point of the ellipse is 10.
In particular, the sum (c+a) PLUS (a-c) from the foci to the right-most vertex of the ellipse is 10:
(c+a) + (a-c) = 10.
It gives 2a = 10; hence, a = 10/2 = 5.
By knowing "a" and "c" of the ellipse, we easily find "b", the length of the minor semi-axis: it is
b = 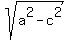 = =  = =  - - 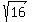 = 4.
Now we are in position to write the standard form equation of this ellipse. It is = 4.
Now we are in position to write the standard form equation of this ellipse. It is
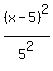 + + 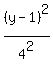 = 1. = 1.
Solved.
----------------------
As you see, on the way of solving this problem I applied some trick, by using the sum of distances to some special point.
This trick is the major key point of the solution to this problem.
//////////////
For basic info about ellipses, see my lesson
- Ellipse definition, canonical equation, characteristic points and elements
in this site.
|
|
|
| |