|
Question 1170522: The cable of suspension bridge hangs in the shape of a parabola. The towers supporting the cable are 400ft apart and 150ft high. If the cable, at its lowest, is 30ft above the bridge at its midpoint, how high is the cable 50ft away (horizontally) from either tower?
Found 3 solutions by CPhill, ikleyn, Edwin McCravy:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**1. Set up a Coordinate System**
* Place the vertex of the parabola (the lowest point of the cable) at the origin (0, 30).
* The towers are 400 feet apart, so they are located at (-200, 150) and (200, 150).
**2. Find the Equation of the Parabola**
* The general equation of a parabola with a vertical axis of symmetry and vertex (h, k) is:
(x - h)^2 = 4p(y - k)
* In our case, the vertex is (0, 30), so the equation becomes:
x^2 = 4p(y - 30)
* We know the towers are at (200, 150). Plug these coordinates into the equation to find 'p':
(200)^2 = 4p(150 - 30)
40000 = 4p(120)
40000 = 480p
p = 40000 / 480 = 83.333... = 250/3
* Now, plug 'p' back into the equation:
x^2 = 4(250/3)(y - 30)
x^2 = (1000/3)(y - 30)
**3. Find the Height 50 Feet from a Tower**
* We want to find the height of the cable 50 feet horizontally from either tower. Since the towers are at x = ±200, we're looking for the height at x = 200 - 50 = 150 and x = -200 + 50 = -150. Due to symmetry, the height will be the same.
* Plug x = 150 (or x = -150) into the parabola equation:
(150)^2 = (1000/3)(y - 30)
22500 = (1000/3)(y - 30)
22500 * (3/1000) = y - 30
67.5 = y - 30
y = 67.5 + 30
y = 97.5
**4. Answer**
* The cable is 97.5 feet high 50 feet away (horizontally) from either tower.
**Final Answer:** 97.5 feet
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The cable of suspension bridge hangs in the shape of a parabola.
The towers supporting the cable are 400 ft apart and 150 ft high.
If the cable, at its lowest is 30 ft above the bridge at its midpoint,
how high is the cable 50 ft away (horizontally) from either tower?
~~~~~~~~~~~~~~~~~~~~~~~~~
If we place the origin of the coordinate system at the bridge level midpoint
between the two towers, we have the vertex of the parabola at the point (0,30).
So, we write an equation of the parabola in vertex form
y = ax^2 + 30.
Coefficient "a" is unknown. It is the only unknown in this problem now.
To find it, we use the condition at the endpoint: y= 150 at x= 400/2 = 200. It gives
150 = a*200^2 + 30
150 - 30 = a*40000
120 = 40000a
a =  = = 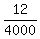 = = 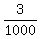 .
Thus the parabola is y = .
Thus the parabola is y = 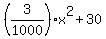 .
To find the level of the cable at 50 ft from the tower, we substitute x = 200-50 = 150 ft
into the equation of the parabola.
This way we get the height of the cable at the point x= 150 ft, which is 50 feet from the tower
y = .
To find the level of the cable at 50 ft from the tower, we substitute x = 200-50 = 150 ft
into the equation of the parabola.
This way we get the height of the cable at the point x= 150 ft, which is 50 feet from the tower
y = 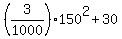 = 97.5 ft. ANSWER = 97.5 ft. ANSWER
Solved.
//////////////////
It can be solved mentally, without using equations, too.
The maximum difference of the levels of the cable is 150 - 30 = 120 ft.
The distance 150 ft from the central point to the tower is 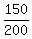 = =  of the half the bridge length.
Hence, the level of the cable at x= 150 ft from the center is
30 +
of the half the bridge length.
Hence, the level of the cable at x= 150 ft from the center is
30 + 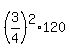 = 30 + = 30 + 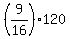 = 30 + = 30 + 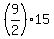 = 30 + 9*7.5 = use your calculator = 97.5 ft,
giving the same answer. = 30 + 9*7.5 = use your calculator = 97.5 ft,
giving the same answer.
///////////////////////////////////
Edwin, regarding your lamentations, don't you think that this AI would have been paid
by the same multi-billionaires (or trillionairs) and you will ELECT it as a highest ruler, without even suspecting it ?
Answer by Edwin McCravy(20055)   (Show Source): (Show Source):
You can put this solution on YOUR website!
As we see, AI is getting better. One day it'll beat us all. I read that it has
been a long time since a human master chess champion was able to beat an AI
computer program programmed to learn from its mistakes.
I just asked AI about that, and got this answer:
AI:
The last time a human world chess champion was able to beat a chess program
designed to learn from its mistakes in a formal match was in 1996, during the
first match between Garry Kasparov and IBM's Deep Blue.
In that match:
Kasparov lost the first game but ultimately won the six-game match 4 - 2. This
victory demonstrated that, while computers were becoming formidable opponents,
humans could still prevail at the highest level of chess.
However, the following year, in 1997, Deep Blue was upgraded and defeated
Kasparov in a highly publicized rematch with a score of 3.5 - 2.5. This marked the
first time a reigning world champion lost a match to a computer under standard
tournament conditions.
Since then, chess engines have continued to improve dramatically, with modern
programs like Stockfish, AlphaZero, and Leela Chess Zero outperforming even the
strongest human players. Today, no human can consistently defeat top chess
engines, which are now considered far superior in both calculation and strategic
understanding.
EM
My question now is: When are we humans going to stop electing selfish multi-
billionaire humans as presidents of countries, as in the present USA, and start
electing AI?
Edwin
|
|
|
| |