Question 1169047: At this point, you are now ready to take the summative assessment for learning plan 3. Place your answers on a whole sheet of paper. Show your complete solution. (20 points)
1. Write the standard form of the equation of the hyperbola with the following characteristics:
Center at (2,3)
Vertices at (-1,3) and (5,3)
Covertices at (2,-2) and (2,8)
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! recal:
Coordinates of the center: ( , ,  ). ).
Coordinates of vertices: (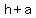 , ,  ) and ( ) and ( , , ) )
Co-vertices correspond to  , the ” minor semi-axis length”, and coordinates of co-vertices: , the ” minor semi-axis length”, and coordinates of co-vertices:
( , ,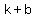 ) and ( ) and ( , ,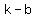 ). ).
Foci have coordinates (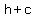 , , ) and ( ) and (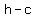 , , ). The value of ). The value of  is given as, is given as,  . .
equation:

given:
Center at ( , , )=( )=( , , ) )
Thus,  , ,  . .
Vertices at ( , , ) and ( ) and ( , , ) )
The distance between the vertices is  . We can find this distance by subtracting the x-coordinates of the vertices: . We can find this distance by subtracting the x-coordinates of the vertices:


so far your equation is:

Covertices at ( , , )and ( )and ( , , ) )
since covertices at ( , ,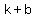 ) and ( ) and ( , ,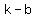 ), we have ), we have
( , ,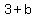 ) =( ) =( , , ) => ) =>  => =>  => =>
so, your equation is:



|
|
|