SOLUTION: Write the standard equation of the parabola given the two endpoints of the focal width ; (-2,3) and (5,3) with p>0

Instead of doing your problem for you, I'll do one exactly like yours step-by-
step.  This is the problem I will do for you.  Use it as a model to do yours by:

The equation has the standard form:

  with p positive

where
the focus is the midpoint between the endpoints of the 
focal chord (also called the latus rectum)
4p = the focal width = distance between the two endpoints
p = the distance from the focus to the vertex 
(h,k) = the vertex, which has the same x-coordinate as the focus.

the focus is the midpoint between (-4,5) and (9,5) which is 


I'll plot the end points of the focal width, and the focus:



4p = the focal width = distance between the two endpoints, 





p = the distance from the focus to the vertex.

So we subtract 13/4 from the y-coordinate of the focus:
The y-coordinate of the focus is 5, so


So the vertex is



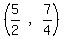I'll plot the vertex:



and sketch in the parabola:



So the standard equation of the parabola is





Now do yours exactly step-by-step the same way.

Edwin