SOLUTION: Find the latus rectum, vertex and directrix of the parabola y^2-8x-2y+17=0

Click here to see ALL problems on Quadratic-relations-and-conic-sections

Question 1129284: Find the latus rectum, vertex and directrix of the parabola y^2-8x-2y+17=0
Found 3 solutions by MathLover1, josgarithmetic, MathTherapy:
Answer by MathLover1(20850)   (Show Source):
You can put this solution on YOUR website!

Find the latus rectum, vertex and directrix of the parabola
...first write it in vertex form

=> compare to form
=> and => vertex is at (, )

focus: (,)= (,)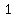
Equation of the directrix is

The line segment that passes through the focus (,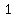) and is parallel to the directrix is called the latus rectum.
The 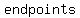of the latus rectum lie on the curve, and they are:
(,) and (,)
since , we have
(,) and (,)
distance between them is the length of the latus rectum:

so, length of the latus rectum =

Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!

Answer by MathTherapy(10552)   (Show Source):
You can put this solution on YOUR website!

Find the latus rectum, vertex and directrix of the parabola y^2-8x-2y+17=0

This is a parabola with a HORIZONTAL AXIS of SYMMETRY, and so, its equation is:
Given equation:
After COMPLETING the SQUARE on y, we get:
Comparing that to the equation of a parabola with a HORIZONTAL AXIS of SYMMETRY, or , we see that:
h = 2; k = 1
4p = 8, or