|
Question 1100161: Suspension Bridge.
If one parabolic segment of a suspension bridge is 400 feet and if the cables at the vertex are suspended 10 feet above the bridge, whereas the height of the cables 200 feet from the vertex reaches 50 feet, find the equation of the parabolic path of the suspension cables.
Enter the equation in standard form.
The equation of the parabolic path of the suspension cables is what?
Found 2 solutions by ankor@dixie-net.com, ikleyn:
Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website! Suspension Bridge.
If one parabolic segment of a suspension bridge is 400 feet and
if the cables at the vertex are suspended 10 feet above the bridge,
whereas the height of the cables 200 feet from the vertex reaches 50 feet,
find the equation of the parabolic path of the suspension cables.
Enter the equation in standard form.
Assuming the left side of the bridge is at the origin
from the information we can create the following pairs
0,50; 200,10; 400,50. Form equations in the form ax^2 + bx + c = y
The first pair 0,50 tells us that c=50
200,10
(200^2)a + 200b + 50 = 10
40000a + 200b = 10 - 50
40000a + 200b = -40
:
400,50
(400^2)a + 400b + 50 = 50
160000a + 400b = 0
:
Use elimination with these two equations, multiply the firs eq by 2
160000a + 400b = 0
80000a + 400b = -80
------------------- subtraction eliminates b, find a
80000a = 80
a = 80/80000
a = .001
find b using the first original equation
40000(.001) + 200b = -40
40 + 200b = -40
200b = -40 - 40
b = -80/200
b = -.4
:
The equation: y = .001x^2 - .4x + 50
Graphically, green is 50 ft, blue is 10 ft
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
If one parabolic segment of a suspension bridge is 400 feet and if the cables at the vertex are suspended 10 feet above the bridge,
whereas the height of the cables 200 feet from the vertex reaches 50 feet, find the equation of the parabolic path of the suspension cables.
Enter the equation in standard form.
The equation of the parabolic path of the suspension cables is what?
~~~~~~~~~~~~~~~~~~~~~
Place the origin of the coordinate system at the bridge level, under the vertex of the cable.
(The term "vertex" is used in the condition, assuming that you know its meaning.
If not, then the vertex is the point where the cable is CLOSEST to the bridge: where the cable is at the minimal level).
In this coordinate system, the cable is a parabola y = ax^2 + b,
where b is exactly the elevation of the lowest point of the cable over the bridge, and "a" is an unknown coefficient.
From the condition, you have b = 10 ft, obviously. So, y = ax^2 + 10.
All you need to do is to find the coefficient "a".
For it, use the condition that at the distance 200 ft from the vetex (along the bridge, naturally) the height of the cable is 50 ft:
50 = a*200^2 + 10.
From this equation a =  =  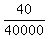= 0.001.
Thus the equation of the parabola is y = 0.001*x^2 + 10,
where x is the distance along the bridge from the vertex position.
That's all. The problem is solved.
|
|
|
| |
