|
Question 1082287: Write an equation for the ellipse, satisfying the following conditions. Foci at (0,-2) and (0,2); the point (3,2) on the ellipse
Found 2 solutions by natolino_2017, ikleyn:
Answer by natolino_2017(77)   (Show Source): (Show Source):
You can put this solution on YOUR website! The mid point between the two focus is the center of the ellipse.
In this case, Center= ((0+0)/2 , (2+-2)/2) =(0 , 0).
Let P = (3 , 2), F1 = (0 , -2), F2 =(0 , 2)
"The sum of the distance of a point of the ellipse to every Focus, is constant and equal to the double of the Semi-major axis (A)"
PF1 + PF2 = 2A.
5 + 3 = 2A
A = 4
Let C: distance from the center to a focus.
C = 2.
A^2 = B^2 + C^2
B = sqrt(12).
So the equation is
x^2/12 + y^2/16 = 1.
observation: the Focus doesn't belong to the ellipse.
@natolino_
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. The center of the ellipse is at (0,0).
The major axis is y-axis x= 0;
Hence, the minor axis is x-axis y= 0.
2. The canonical equation of this ellipse is
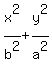 = 1 (it is written in the form to fit the fact that the major axis is y-axis: a > b > 0)
Since the point (3,2) is on the ellipse, it implies = 1 (it is written in the form to fit the fact that the major axis is y-axis: a > b > 0)
Since the point (3,2) is on the ellipse, it implies
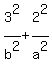 = 1, or = 1, or
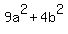 = = 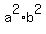 . (1)
3. The focal distance is 2c = 2 - (-2) = 4.
Hence, the linear eccentricity c = . (1)
3. The focal distance is 2c = 2 - (-2) = 4.
Hence, the linear eccentricity c =  = 2. It means that = 2. It means that
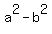 = 4. (2)
4. Thus you have two equations (1) and (2) to determine "a" and "b".
You can simplify writing and solving by introducing new variables x = = 4. (2)
4. Thus you have two equations (1) and (2) to determine "a" and "b".
You can simplify writing and solving by introducing new variables x =  and y = and y =  :
9x + 4y = xy (3) instead of (1), and
x - y = 4. (4) instead of (2)
The setup is done.
Now it is simple arithmetic to solve it and to get "a" and "b" at the end.
4. From (4), x = 4 + y, Substitute it into (3). You will get
9(4+y) + 4y = (4+y)*y,
36 + 9y + 4y = 4y + y^2 ---> y^2 -9y - 36 = 0 ----> :
9x + 4y = xy (3) instead of (1), and
x - y = 4. (4) instead of (2)
The setup is done.
Now it is simple arithmetic to solve it and to get "a" and "b" at the end.
4. From (4), x = 4 + y, Substitute it into (3). You will get
9(4+y) + 4y = (4+y)*y,
36 + 9y + 4y = 4y + y^2 ---> y^2 -9y - 36 = 0 ----> 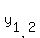 = = 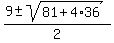 = = 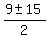 .
Only positive root works: y = 12. So, .
Only positive root works: y = 12. So,  = 12 and b = = 12 and b =  .
Then a^2 = b^2 + 4 = 12 + 4 = 16 and a = .
Then a^2 = b^2 + 4 = 12 + 4 = 16 and a = 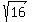 = 4.
Thus semi-axes are 4 (vertical) and = 4.
Thus semi-axes are 4 (vertical) and  (horizontal).
The equation for the ellipse is (horizontal).
The equation for the ellipse is
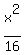 + + 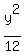 = 1. = 1.
As a prerequisite, see the lesson
- Ellipse definition, canonical equation, characteristic points and elements
in this site.
Also, you have this free of charge online textbook in ALGEBRA-II in this site
ALGEBRA-II - YOUR ONLINE TEXTBOOK.
The referred lesson is the part of this online textbook under the topic
"Conic sections: Ellipses. Definition, major elements and properties. Solved problems".
|
|
|
| |