SOLUTION: Write the equation of a hyperbola with vertices at (1,1) and (9, 1) and foci at (0, 1) and (10, 1).

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: Write the equation of a hyperbola with vertices at (1,1) and (9, 1) and foci at (0, 1) and (10, 1).      Log On


   

Question 1068143: Write the equation of a hyperbola with vertices at (1,1) and (9, 1) and foci at (0, 1) and (10, 1).
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The equation of a hyperbola involves numbers that we call
h , k , c , a , and b .
We have to find those values.
We realize that vertices and foci are all on a line with y=1 .
The hyperbola looks like this: ) ( ,
and with the line y=1 it looks like this: ----)--(---- .
All the important points of the hyperbola have the same y-coordinate,
and that makes all calculations easy.
That y=1 line TRAVERSES all those points.
The segment of that line connecting the vertices
is called the traNsverse axis of the hyperbola
(watch for that N when you spell the word).
The center of a hyperbola (or of an ellipse)
is the midpoint of that segment connecting the vertices.
It is also the midpoint of the segment connecting the foci.
We call that point 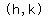%22%28+h+%2C+k+%29%22 .
In this case, it is easiest to see the center of this hyperbola
as the point halfway between foci (0,1) and (10,1) ,
point (5,1), with system%28x=5%2Cy=1%29 .
That calculation is easy mental math.
If someone wanted to see the calculation on paper,
the coordinates of that midpoint are the averages of the coordinates of the foci:
h=%280%2B10%29%2F2=10%2F2=5 and k=%281%2B1%29%2F2=2%2F2=1 .
So, we have highlight%28system%28h=5%2Ck=1%29%29 .
The distance from the center of a hyperbola (or of an ellipse) to each focus
is called the focal distance, c .
In this case highlight%28c=5%29=5-0 , the distance from center (5,1), to focus (0,1).
The distance from the center of a hyperbola (or of an ellipse) to each vertex
is called a .
In this case highlight%28a=4%29=5-1 , the distance from center center (5,1), to vertex (1,1).
The number b (for a hyperbola, or for an ellipse)
is the distance from the center to points called co-vertices.
In a hyperbola, the numbers (or distances) c , a , and b
are lengths of sides of a right triangle,
related by b%5E2%2Ba%5E2=c%5E2 .
In this case, b%5E2%2B4%5E2=5%5E2 ,
so b%5E2%2B16=25 <--> b%5E2%2B16=25 <--> b%5E2=9 <--> highlight%28b=3%29 .
Now, we can write the equation of the hyperbola as
%28x-h%29%5E2%2Fa%5E2-%28y-k%29%5E2%2Fb%5E2=1 .
Substituting the number values we found for h , k , c , a , and b ,
the equation is
highlight%28%28x-5%29%5E2%2F4%5E2-%28y-1%29%5E2%2F3%5E2=1%29 or highlight%28%28x-5%29%5E2%2F16-%28y-1%29%5E2%2F9=1%29 .
Some hyperbolas have equations of the form
-%28x-h%29%5E2%2Fb%5E2%2B%28y-k%29%5E2%2Fa%5E2=1 or %28y-k%29%5E2%2Fa%5E2-%28x-h%29%5E2%2Fb%5E2=1 ,
but when a coordinate value (like y=1 ) is hared by vertices, foci, and center of a hyperbola,
the term with that coordinate gets the minus sign and the b .