|
Tutors Answer Your Questions about Quadratic-relations-and-conic-sections (FREE)
Question 1168977: Conjugate axis along the y-axis, ome vertex at (0,7), asymptotes are 6x-5y+30=0 and 6x+5y-30=0. Need help finding the Equation of this hyperbola. How?
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Conjugate axis along the y-axis, one vertex at (0,7), asymptotes are 6x-5y+30=0 and 6x+5y-30=0.
Need help finding the Equation of this hyperbola. How?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Regarding this post, I have two notices.
First notice is that the problem's formulation is INCORRECT and SELF-CONTRADICTORY.
It describes a situation which NEVER may happen in reality.
Indeed, the problem says that conjugate axis of the hyperbola is along y-axis,
one vertex is (0,7) and the asymptotes are 6x-5y+30 = 0 and 6x+5y-30 = 0.
From equations, the center of the hyperbola is (x,y) = (0,6).
Together with the information about " one vertex ", it means that transverse axis is vertical y-axis,
and it contradicts that the conjugate axis is y-axis, as stated in the post.
It disproves the problem, kills it to the death and ruins it into dust.
Second notice is that the solution in the post by @CPhill is TOTALLY and FATALLY incorrect,
starting from his first two lines, where he writes an equation of the hyperbola in WRONG FORM.
So, the problem itself is  , as well as its " solution " produced and presented by @CPhill. , as well as its " solution " produced and presented by @CPhill.
For the peace in your mind, my dear reader, ignore both the problem and its " solution " by @CPhill.
A right place for such compositions is a trash bin.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
The equation of a hyperbola with a conjugate axis along the y-axis has the standard form:
$\frac{(y-k)^2}{a^2} - \frac{(x-h)^2}{b^2} = 1$
where $(h, k)$ is the center of the hyperbola, $2a$ is the length of the transverse axis, and $2b$ is the length of the conjugate axis.
The asymptotes of this hyperbola are given by:
$y - k = \pm \frac{a}{b}(x - h)$
We are given the equations of the asymptotes as $6x - 5y + 30 = 0$ and $6x + 5y - 30 = 0$. We can rewrite these in the slope-intercept form ($y = mx + c$):
$5y = 6x + 30 \implies y = \frac{6}{5}x + 6$
$5y = -6x + 30 \implies y = -\frac{6}{5}x + 6$
The slopes of the asymptotes are $\pm \frac{6}{5}$. Therefore, $\frac{a}{b} = \frac{6}{5}$.
The intersection of the asymptotes gives the center of the hyperbola. We can solve the system of equations:
$y = \frac{6}{5}x + 6$
$y = -\frac{6}{5}x + 6$
Setting them equal: $\frac{6}{5}x + 6 = -\frac{6}{5}x + 6 \implies \frac{12}{5}x = 0 \implies x = 0$.
Substituting $x=0$ into either equation gives $y = 6$.
So, the center of the hyperbola is $(h, k) = (0, 6)$.
We are given that one vertex is at $(0, 7)$. For a hyperbola with a vertical transverse axis and center $(0, 6)$, the vertices are at $(0, k \pm a) = (0, 6 \pm a)$.
Since one vertex is at $(0, 7)$, we have $6 + a = 7$ or $6 - a = 7$.
If $6 + a = 7$, then $a = 1$.
If $6 - a = 7$, then $a = -1$, which is not possible for the length $a$.
Thus, $a = 1$, and $a^2 = 1$.
Now we use the relationship $\frac{a}{b} = \frac{6}{5}$ with $a = 1$:
$\frac{1}{b} = \frac{6}{5} \implies b = \frac{5}{6}$.
So, $b^2 = \left(\frac{5}{6}\right)^2 = \frac{25}{36}$.
The equation of the hyperbola is:
$\frac{(y - 6)^2}{a^2} - \frac{(x - 0)^2}{b^2} = 1$
$\frac{(y - 6)^2}{1} - \frac{x^2}{\frac{25}{36}} = 1$
$(y - 6)^2 - \frac{36x^2}{25} = 1$
Final Answer: The final answer is $\boxed{(y - 6)^2 - \frac{36x^2}{25} = 1}$
Question 1209794: (x+4)^2/9+(y+3)^2 /4 =1
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
It looks like the Artificial Intelligence (represented by @CPhill) reached a dead end and cannot answer correctly.
Meanwhile, the answer is simple:
This equation represents an ellipse with the center at the point (-4,-3)
with a major semi-axis of  = 3 units (horizontal) and a minor semi-axis of = 3 units (horizontal) and a minor semi-axis of  = 2 units (vertical). = 2 units (vertical).
Question 1167285: A router is in the library of the university which is 1.5 years away from a student lounge. The range of the router, which services the WIFI connection of the university, has a diameter of 3.5 meters, with it as the center. Can students staying in the lounge connect to the said WIFI?
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1167416: The tower stands 180 meters tall. The diameter of the top is 75 meters. At their closest, the sides of the tower are 60 meters apart. Find the equation of the hyperbola that models the sides of the cooling tower. Assume that the center of the hyperbola is the origin. Round of final answer to the nearest whole number.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The tower stands 180 meters tall. The diameter of the top is 75 meters. At their closest,
the sides of the tower are 60 meters apart. Find the equation of the hyperbola that models
the sides of the cooling tower. Assume that the center of the hyperbola is the origin.
Round of final answer to the nearest whole number.
~~~~~~~~~~~~~~~~~~~~~~~~~~
The problem in the post is posed INCORRECTLY.
In the form as it is presented in the post, the problem CAN NOT be solved,
since the given input information is not sufficient.
As the problem is presented, it is clear that the problem's creator is absolutely
(i.e. TOTALLY) illiterate in the subject.
In this form, this task is simply a misunderstanding,
and its appearance on the forum is an unfortunate accident.
In order for the equation of a hyperbola could be restored, the positions (= the coordinates)
of its three points should be given. But in this post, this info is not provided.
It could be solved, if the height of the narrowest part be given; but this info is MISSED in the problem.
The lowest possible score to the problem's creator for his or her unsatisfactory job.
Question 1167713: 1. Kepler observed that Pluto orbits the sun in an elliptic motion. With the
sun at one focus, nearest that Pluto gets to the Sun is 4,400,000,000 km, and the farthest that it goes to the Sun is 7,400,000,000 km.
a) Assuming that the center of Pluto’s orbit is at (0, 0), find the equation
that models Pluto’s orbit.
b) If an unidentified planet is located in the other focus, how far is this
planet from the Sun?
Found 2 solutions by ikleyn, htmentor:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1. Kepler observed that Pluto orbits the sun in an elliptic motion. With the
sun at one focus, nearest that Pluto gets to the Sun is 4,400,000,000 km, and the farthest that it goes to the Sun is 7,400,000,000 km.
a) Assuming that the center of Pluto’s orbit is at (0, 0), find the equation
that models Pluto’s orbit.
b) If an unidentified planet is located in the other focus, how far is this
planet from the Sun?
~~~~~~~~~~~~~~~~~~~~~~~~~~~
The problem's formulation is MONSTROUS.
To part (a)
Kepler lived 1571 - 1630.
Pluto was discovered in the year 1930.
So, Kepler (as a person) could not observe Pluto and did not know about Pluto's existence.
To part (b)
If another planet is " placed " in the other focus (in the standard meaning of the word " placed "),
then, according to Physics, this planet will fall to the Sun.
So, this formulation in (b) is MONSTROUS, too.
Answer by htmentor(1343)   (Show Source): (Show Source):
You can put this solution on YOUR website! The equation for an ellipse centered at the origin is x^2/a^2 + y^2/b^2 = 1, where a, b are the semi-major and semi-minor axes, respectively.
The sun is located at one focus with coordinates (-c,0), with c^2 = a^2 - b^2.
For simplicity, we will express the distances in billions of miles.
The distance of the furthest approach is 7.4 = c + a, and the closest
approach is 4.4 = a - c. Solving for a gives 2a = 11.8 -> a = 5.9.
Solving for c gives 2c = 3 -> c = 1.5.
b^2 = a^2 - c^2 -> b^2 = 5.9^2 - 1.5^2 = 32.56.
Thus, the equation is x^2/34.81 + y^2/32.56 = 1.
If another planet is placed at the other focus, the distance between them
will be 2c = 3.
Question 1168412: The Bayonne bridge connects Staten Island, New York to New Jersey. It has an arch in the shape of parabola that opens downward. Write an equation of the parabola to model the arch, assuming that the origin is at the surface of the water. 325. ft and 1675ft
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem and find the equation of the parabola.
**1. Understand the Problem**
* The arch of the Bayonne Bridge is in the shape of a downward-opening parabola.
* The origin (0, 0) is at the surface of the water.
* We are given two key dimensions:
* The width of the arch at the water's surface is 1675 feet.
* The height of the arch is 325 feet.
**2. Set Up the Vertex**
* Since the parabola opens downward and the origin is at the water's surface, the vertex of the parabola will be at the highest point of the arch.
* The vertex will be located at (1675/2, 325) = (837.5, 325).
**3. General Equation of a Parabola**
The general equation of a parabola with a vertical axis of symmetry is:
y = a(x - h)² + k
Where:
* (h, k) is the vertex of the parabola.
* 'a' determines the direction and width of the parabola.
**4. Plug in the Vertex**
* We know the vertex is (837.5, 325), so h = 837.5 and k = 325.
* The equation becomes:
y = a(x - 837.5)² + 325
**5. Find 'a'**
* We know the parabola passes through the origin (0, 0). Plug in x = 0 and y = 0:
0 = a(0 - 837.5)² + 325
0 = a(837.5)² + 325
-325 = a(837.5)²
a = -325 / (837.5)²
a = -325 / 701406.25
a ≈ -0.00046335
**6. Write the Equation**
* Substitute the value of 'a' back into the equation:
y = -0.00046335(x - 837.5)² + 325
**7. Simplify (Optional)**
* If needed, we can round 'a' to a more manageable value:
y ≈ -0.000463(x - 837.5)² + 325
**Therefore, the equation of the parabola that models the arch of the Bayonne Bridge is approximately y = -0.000463(x - 837.5)² + 325.**
Question 1165099: A cable hangs in the form of a branch of a hyperbola between two poles that are 20 meters apart. The poles
are 70 meters high and the cable has a sag of 2 meters midway between the poles. Find the height of the cable
at a point 3 meters from one of the poles.
PLEASE HELP ME HUHUHU. THANK YOU SO MUCH!!
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Usually, in such problem a shape of a parabola is considered - not a shape of hyperbola.
Therefore, throw your problem to the closest garbage bin, where its natural place is.
Let will not multiply the amount of gibberish in the Internet.
Question 1168931: Find the (standard) equation of the hyperbola whose foci are 𝐹1(-3,0) and 𝐹2(3,0),
such that for any point on it, the absolute value of the difference of its distances
from the foci is 3.
Found 2 solutions by ikleyn, MathLover1:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the (standard) equation of the hyperbola whose foci are 𝐹1(-3,0) and 𝐹2(3,0),
such that for any point on it, the absolute value of the difference of its distances from the foci is 3.
~~~~~~~~~~~~~~~~~~~~~~~
The solution by @MathLover1 is INCORRECT.
I came to bring a correct solution.
Since the foci are F1(-3,0) and F2(3,0), we conclude that
- the major axis is horizontal y= 0 and coincides with x-axis;
- the center is at (0,0), half way between the foci;
- the distance between the foci is 3 - (-3) = 6 units and the distance
from the center to the foci c = 6/2 = 3 units.
So, the general equation of the hyperbola is
 - -  = 1,
where a > 0 is the horizontal transfer semi-axis.
Now consider this condition "for any point on it, the absolute value of the difference of its distances from the foci is 3.".
We know that 'a' is the distance along x-axis from the center (0,0) to any of the two vertices of the hyperbola.
Then the points (-a,0) and (a,0) are the points on this hyperbola.
For point (a,0), the distance from F1 is (3-a); the distance from F2 is (a+3).
The difference of these distance must be 3, according to the condition.
So, we write this equation
(a+3) - (3-a) = 3,
2a = 3,
a = 3/2 = 1.5.
So, the vetices are at (-1.5,0) and (1.5,0), and 'a', as we found, is 1.5.
Then from equation a^2 + b^2 = c^2 we can find 'b^2'
1.5^2 + b^2 = 3^2
b^2 = 3^2 - 1.5^2 = 9 - 2.25 = 6.75.
Hence, the standard equation of this hyperbola is = 1,
where a > 0 is the horizontal transfer semi-axis.
Now consider this condition "for any point on it, the absolute value of the difference of its distances from the foci is 3.".
We know that 'a' is the distance along x-axis from the center (0,0) to any of the two vertices of the hyperbola.
Then the points (-a,0) and (a,0) are the points on this hyperbola.
For point (a,0), the distance from F1 is (3-a); the distance from F2 is (a+3).
The difference of these distance must be 3, according to the condition.
So, we write this equation
(a+3) - (3-a) = 3,
2a = 3,
a = 3/2 = 1.5.
So, the vetices are at (-1.5,0) and (1.5,0), and 'a', as we found, is 1.5.
Then from equation a^2 + b^2 = c^2 we can find 'b^2'
1.5^2 + b^2 = 3^2
b^2 = 3^2 - 1.5^2 = 9 - 2.25 = 6.75.
Hence, the standard equation of this hyperbola is
 - - 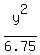 = 1. <<<---=== ANSWER = 1. <<<---=== ANSWER
Solved correctly.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
given:
foci are F1( , , ) and F2( ) and F2( , , ), ),
such that for any point on it, the absolute value of the difference of its distances from the foci is 
The standard form of a hyperbola with a horizontal transverse axis is

where ( , , ) is the center of the hyperbola ) is the center of the hyperbola
 is the distance from the center to a vertex is the distance from the center to a vertex
 is the distance from the center to a co-vertex is the distance from the center to a co-vertex
The center of the hyperbola is the midpoint of the line segment between the foci, which is


so, the center of the hyperbola is at ( , , ) )
The distance between the foci is  , so , so  => =>
The distance from each focus to the center is 
.
using  find find 



So, the equation of the hyperbola is:

since  , this is , this is  a valid hyperbola a valid hyperbola
The foci and vertices coincide, so the hyperbola degenerates into a line.
The hyperbola with the given parameters doesn't exist.
Question 1168800: Write an equation in standard form of the parabola that has the same shape as the graph of
f(x)= 4x^2 or
g(x)=−4x2, but with the given maximum or minimum.
Maximum=7 at x=-2
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1168877: Find the length of latus rectum (LR) is 10, vertex at the origin; parabola opens to the right.
Answer by MathLover1(20849)   (Show Source): (Show Source):
Question 1168920: Find the equation of the ellipse if the endpoints of minor axis are (1,3) and (1,-1) with a focus at (-1,1).Express your answer in general form.
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The equation of an ellipse can be given as,

where
' ' represents the semi-major axis (half of the length of the major axis) ' represents the semi-major axis (half of the length of the major axis)
' ' represents the semi-minor axis (half of the length of the minor axis) ' represents the semi-minor axis (half of the length of the minor axis)
‘ ’ represents the ’ represents the  coordinate of the center coordinate of the center
‘ ’ represents the ’ represents the  coordinate of the center coordinate of the center
if the endpoints of minor axis are ( , , ) and ( ) and ( , , ) , minor axis length is equal to the distance between them which is ) , minor axis length is equal to the distance between them which is 
half of the length of the minor axis is 
=> the center mast be half way between endpoints, and it is at ( , , ) )
a focus at ( , , ) )
the distance between foci ( , , ) and center ( ) and center ( , , ) )
focus is  units from the center, so units from the center, so 
using the Pythagorean fact of all ellipses


so, your formula is


Question 1168978: Foci at (-1,4) and (7,4), transverse axis has the length 8/3. Whats the equation
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
The given information indicates that the conic section is a hyperbola because we are given foci and a transverse axis length.
The foci are at $F_1(-1, 4)$ and $F_2(7, 4)$.
The transverse axis has a length of $\frac{8}{3}$.
From the foci, we can determine the center of the hyperbola as the midpoint of the foci:
Center $(h, k) = \left( \frac{-1 + 7}{2}, \frac{4 + 4}{2} \right) = \left( \frac{6}{2}, \frac{8}{2} \right) = (3, 4)$.
The distance between the foci is $2c$.
$2c = \sqrt{(7 - (-1))^2 + (4 - 4)^2} = \sqrt{(8)^2 + (0)^2} = \sqrt{64} = 8$.
So, $c = 4$.
The length of the transverse axis is $2a$. We are given $2a = \frac{8}{3}$, so $a = \frac{4}{3}$.
Since the y-coordinates of the foci are the same, the transverse axis is horizontal. The standard form of the equation of a hyperbola with a horizontal transverse axis and center $(h, k)$ is:
$\frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} = 1$
We need to find $b^2$. We use the relationship $c^2 = a^2 + b^2$ for a hyperbola.
$4^2 = \left(\frac{4}{3}\right)^2 + b^2$
$16 = \frac{16}{9} + b^2$
$b^2 = 16 - \frac{16}{9} = \frac{144 - 16}{9} = \frac{128}{9}$.
Now, substitute the values of $h=3$, $k=4$, $a^2 = \left(\frac{4}{3}\right)^2 = \frac{16}{9}$, and $b^2 = \frac{128}{9}$ into the standard form:
$\frac{(x - 3)^2}{\frac{16}{9}} - \frac{(y - 4)^2}{\frac{128}{9}} = 1$
Multiply the numerators by $\frac{9}{16}$ and $\frac{9}{128}$ respectively:
$\frac{9(x - 3)^2}{16} - \frac{9(y - 4)^2}{128} = 1$.
Final Answer: The final answer is $\boxed{\frac{9(x - 3)^2}{16} - \frac{9(y - 4)^2}{128} = 1}$
Question 1169000: find the equation of the ellipse if the vertex is at (5,1) and foci at (-2,1) and (4,1). express your answer in general form.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Solution:
The given information about the ellipse is:
Vertex: $(5, 1)$
Foci: $(-2, 1)$ and $(4, 1)$
Since the y-coordinates of the vertex and the foci are the same, the major axis of the ellipse is horizontal.
The center of the ellipse is the midpoint of the foci:
Center $(h, k) = \left( \frac{-2 + 4}{2}, \frac{1 + 1}{2} \right) = \left( \frac{2}{2}, \frac{2}{2} \right) = (1, 1)$
The distance between the center and a focus is $c$. Using the focus at $(4, 1)$:
$c = \sqrt{(4 - 1)^2 + (1 - 1)^2} = \sqrt{3^2 + 0^2} = \sqrt{9} = 3$
The distance between the center and a vertex is $a$. Using the vertex at $(5, 1)$:
$a = \sqrt{(5 - 1)^2 + (1 - 1)^2} = \sqrt{4^2 + 0^2} = \sqrt{16} = 4$
We know the relationship between $a$, $b$, and $c$ for an ellipse: $c^2 = a^2 - b^2$.
Substituting the values of $a$ and $c$:
$3^2 = 4^2 - b^2$
$9 = 16 - b^2$
$b^2 = 16 - 9 = 7$
The standard form of the equation of a horizontal ellipse with center $(h, k)$ is:
$\frac{(x - h)^2}{a^2} + \frac{(y - k)^2}{b^2} = 1$
Substituting the values of $h=1$, $k=1$, $a^2 = 16$, and $b^2 = 7$:
$\frac{(x - 1)^2}{16} + \frac{(y - 1)^2}{7} = 1$
To express the equation in general form, we eliminate the denominators and expand:
$7(x - 1)^2 + 16(y - 1)^2 = 16 \times 7$
$7(x^2 - 2x + 1) + 16(y^2 - 2y + 1) = 112$
$7x^2 - 14x + 7 + 16y^2 - 32y + 16 = 112$
$7x^2 + 16y^2 - 14x - 32y + 23 = 112$
$7x^2 + 16y^2 - 14x - 32y + 23 - 112 = 0$
$7x^2 + 16y^2 - 14x - 32y - 89 = 0$
Final Answer: The final answer is $\boxed{7x^2 + 16y^2 - 14x - 32y - 89 = 0}$
Question 1169047: At this point, you are now ready to take the summative assessment for learning plan 3. Place your answers on a whole sheet of paper. Show your complete solution. (20 points)
1. Write the standard form of the equation of the hyperbola with the following characteristics:
Center at (2,3)
Vertices at (-1,3) and (5,3)
Covertices at (2,-2) and (2,8)
Answer by MathLover1(20849)   (Show Source): (Show Source):
You can put this solution on YOUR website! recal:
Coordinates of the center: ( , ,  ). ).
Coordinates of vertices: (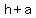 , ,  ) and ( ) and ( , , ) )
Co-vertices correspond to  , the ” minor semi-axis length”, and coordinates of co-vertices: , the ” minor semi-axis length”, and coordinates of co-vertices:
( , ,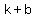 ) and ( ) and ( , ,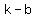 ). ).
Foci have coordinates (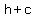 , , ) and ( ) and (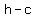 , , ). The value of ). The value of  is given as, is given as,  . .
equation:

given:
Center at ( , , )=( )=( , , ) )
Thus,  , ,  . .
Vertices at ( , , ) and ( ) and ( , , ) )
The distance between the vertices is  . We can find this distance by subtracting the x-coordinates of the vertices: . We can find this distance by subtracting the x-coordinates of the vertices:


so far your equation is:

Covertices at ( , , )and ( )and ( , , ) )
since covertices at ( , ,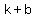 ) and ( ) and ( , ,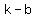 ), we have ), we have
( , ,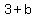 ) =( ) =( , , ) => ) =>  => =>  => =>
so, your equation is:



Question 1169036: find the equation of the ellipse if the endpoints of minor axis are (1,3) and (1,-1) with a focus at (-1,1).
Answer by mccravyedwin(407)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Notice that on the first page this problem reads this way:
Quadratic-relations-and-conic-sections/1169036 (2020-11-05 01:23:06):
See the " 2020-11-05 01:23:06 "? This means that this problem was posted by a
student 4 1/2 years ago on November 5, 2020 at 1:23:06 AM. The student who
posted this is no doubt long gone from the class he or she was taking back in
2020, and is no longer a student.
Back in 2020 there were still lots of algebra and trig problems being posted.
There weren't enough tutors on here, and many problems like this one scrolled
off before the tutors got around to solving them because there were so many.
But then the schools learned that kids can take basic statistics with almost no
knowledge of second year algebra, no geometry, or trig. First year algebra
is enough mathematics for basic statistics, especially now since it's mostly all
done on computers.
So apparently, now most high school students take statistics instead of trig and
college algebra. That's why practically all posts on here nowadays are
statistics problems.
OK, I'll shut up and do this problem posted back in 2020. The former students
getting solutions in their emails to problems they posted back in 2020 are
probably having a good laugh! J
----------------------
Find the equation of the ellipse if the endpoints of minor axis are (1,3) and
(1,-1) with a focus at (-1,1).
First draw what is given, the minor axis, and plot a focus at (-1,1).
 Since the minor axis is vertical, we know that the major axis is horizontal,
and the ellipse is like the cross section of an egg sitting on a table, [and
not like the number 0, when the minor axis is horizontal and the major axis is
vertical.] So the length of the semi-major axis ' a ' goes under the term with
x, and the length of the semi-minor axis ' b ' goes under the term with y. So
the form of the equation is
Since the minor axis is vertical, we know that the major axis is horizontal,
and the ellipse is like the cross section of an egg sitting on a table, [and
not like the number 0, when the minor axis is horizontal and the major axis is
vertical.] So the length of the semi-major axis ' a ' goes under the term with
x, and the length of the semi-minor axis ' b ' goes under the term with y. So
the form of the equation is
 Where the center is the point (h,k).
Next, we draw the center, which is the midpoint of the minor axis. We can tell
the center is the point (1,1).
Where the center is the point (h,k).
Next, we draw the center, which is the midpoint of the minor axis. We can tell
the center is the point (1,1).
 so we know that the center (h,k) = (1,1).
So we have everything but ' a '. So we can write this much of the equation:
so we know that the center (h,k) = (1,1).
So we have everything but ' a '. So we can write this much of the equation:
 No we calculate ' a '.
The value " c " is the distance from the center to a focus. We can tell that the
distance from the center (0,0) to a focus (-1,1) is 2 units, so the value of
c = 2. Then we use the Pythagorean fact of all ellipses, which is
No we calculate ' a '.
The value " c " is the distance from the center to a focus. We can tell that the
distance from the center (0,0) to a focus (-1,1) is 2 units, so the value of
c = 2. Then we use the Pythagorean fact of all ellipses, which is
 where
a is the length of the semi-major axis,
b is the length of the semi-minor axis, and
c is the distance from the center to a focus.
Since the minor axis that we drew is 4 units long, the semi-minor axis, b, is
half that, or b=2. So we substitute b=2 and c=2 into where
a is the length of the semi-major axis,
b is the length of the semi-minor axis, and
c is the distance from the center to a focus.
Since the minor axis that we drew is 4 units long, the semi-minor axis, b, is
half that, or b=2. So we substitute b=2 and c=2 into



 So now we know the equation is
So now we know the equation is
 or
or
 <----ANSWER!
But let's finish drawing the ellipse, because you will be asked to do that: <----ANSWER!
But let's finish drawing the ellipse, because you will be asked to do that:
 which is about 2.8.
So draw the major axis, which goes from about 2.8 units left of the center,
to about 2.8 units right of the center. which is about 2.8.
So draw the major axis, which goes from about 2.8 units left of the center,
to about 2.8 units right of the center.
 Now we can sketch in the ellipse.
Now we can sketch in the ellipse.
 And we might as well plot the other focus which is 2 units on the right of the
center.
And we might as well plot the other focus which is 2 units on the right of the
center.
 Edwin
Edwin
Question 1167082: a flashlight is shaped like a paraboloid so that if its bulb is places at then focus, the light rays from the bulb will then bounce off the surface in a focused direction that is parallel to the x-axis. if the paraboloid has a depth of 1.8 inches and the diameter on its surface is 6 inches, how far should the light source be placed from the vertex
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1167899: Please answer this question, I tried but I don't understand it.
Suppose a designer of a 10 ft. parabolic solar cooker wants to place the cooking pot 5 ft. above the vertex. For reference, the first considers a parabolic string with a base 10 ft. and a focus at 5 ft.from the vertex. How deep is the parabolic solar cooker?
Thank you for your help!
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Please answer this question, I tried but I don't understand it.
Suppose a designer of a 10 ft. parabolic solar cooker wants to place the cooking pot 5 ft. above the vertex.
For reference, the first considers a parabolic string with a base 10 ft. and a focus at 5 ft. from the vertex.
How deep is the parabolic solar cooker?
Thank you for your help!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
In this problem, you are given the size 10 ft of the opening of the parabolic solar cooker,
and the distance 5 ft from the vertex to the focus of the paraboloid (same as the place for cooking).
They want you find the depth of the parabolic mirror.
S O L U T I O N
To solve such problems, use an equation of the parabolic cross-section (which is a parabola)
in the form
y = 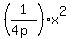 . (1)
In this form, 'p' is the focal distance, i.e. the distance of 5 ft from the vertex
to the cooking place; x is half of the opening, i.e. 10/2 = 5 ft; y is the depth of the paraboloid.
So, we substitute p = 5 ft and x = 5 ft into equation (1), and we get
y = . (1)
In this form, 'p' is the focal distance, i.e. the distance of 5 ft from the vertex
to the cooking place; x is half of the opening, i.e. 10/2 = 5 ft; y is the depth of the paraboloid.
So, we substitute p = 5 ft and x = 5 ft into equation (1), and we get
y =  = =  = =  ft = 1 ft = 1 ft.
At this point, the problem is completely solved.
ANSWER. The depth of the paraboloid is 1 ft.
At this point, the problem is completely solved.
ANSWER. The depth of the paraboloid is 1 ft. ft.
Solved.
Question 1165710: A cable hangs in the form of a branch of a hyperbola between two poles that are 20 meters apart. The poles are 70 meters high and the cable has a sag of 2 meters midway between the poles. Find the height of the cable at a point 3 meters from one of the poles.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A cable hangs in the form of a branch of a hyperbola between two poles that are 20 meters apart.
The poles are 70 meters high and the cable has a sag of 2 meters midway between the poles.
Find the height of the cable at a point 3 meters from one of the poles.
~~~~~~~~~~~~~~~~~~~~~~~~~~
Usually/traditionally, in such problems, a parabolic form is considered,
because parabolic form better corresponds to Physics.
Let's not multiply the amount of gibberish in this world.
Question 1165555: A cable hangs in the form of a branch of a hyperbola between two poles that are 20 meters apart. The poles
are 70 meters high and the cable has a sag of 2 meters midway between the poles. Find the height of the cable
at a point 3 meters from one of the poles.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A cable hangs in the form of a branch of a hyperbola between two poles that are 20 meters apart. The poles
are 70 meters high and the cable has a sag of 2 meters midway between the poles. Find the height of the cable
at a point 3 meters from one of the poles.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Usually/traditionally, in such problems, a parabolic form is considered,
because parabolic form better corresponds to Physics.
Let's not multiply the amount of gibberish in this world.
Question 1169787: Two long-range navigation stations A and B lie on a line running east and west,
and A is 88 miles due east of B. An airplane is travelling east on a straight line course
that is 66 miles north of the line tough A and B. Signals are sent at the same time
from A and B, and the signal from A reaches the plane 350 microseconds before
the one from B. If the signals travel at the rate of 0.2 mile/microsecond, locate the
position of the plane.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this navigation problem step-by-step.
**Understanding the Problem**
We have two navigation stations A and B, and an airplane flying on a parallel course. We're given the distance between A and B, the airplane's distance from the line AB, the time difference in signal reception, and the signal speed. We need to find the airplane's position.
**Diagram**
1. Draw a horizontal line representing the line passing through stations A and B.
2. Mark point B on the left and point A on the right, with a distance of 88 miles between them.
3. Draw a horizontal line 66 miles above the line AB, representing the airplane's path.
4. Let P be the position of the airplane.
5. Draw lines PA and PB.
6. Draw a line from P perpendicular to AB, intersecting AB at point C.
**Given Information**
* Distance AB = 88 miles
* Airplane's distance from line AB (PC) = 66 miles
* Time difference (Δt) = 350 microseconds
* Signal speed (v) = 0.2 mile/microsecond
**Solution**
1. **Distance Difference:**
* The difference in distances traveled by the signals is:
* Δd = v * Δt = 0.2 miles/microsecond * 350 microseconds = 70 miles
* Therefore, PB - PA = 70 miles.
2. **Coordinates:**
* Let B be the origin (0, 0).
* Then A is at (88, 0).
* Let P be at (x, 66).
* Then C is at (x, 0).
3. **Distances PA and PB:**
* PA = √((x - 88)² + 66²)
* PB = √(x² + 66²)
4. **Equation:**
* PB - PA = 70
* √(x² + 66²) - √((x - 88)² + 66²) = 70
5. **Solve for x:**
* √(x² + 66²) = 70 + √((x - 88)² + 66²)
* Square both sides:
* x² + 66² = 4900 + 140√((x - 88)² + 66²) + (x - 88)² + 66²
* x² = 4900 + 140√((x - 88)² + 66²) + x² - 176x + 88²
* 176x - 4900 - 88² = 140√((x - 88)² + 66²)
* 176x - 4900 - 7744 = 140√((x - 88)² + 4356)
* 176x - 12644 = 140√((x - 88)² + 4356)
* (176x - 12644) / 140 = √((x - 88)² + 4356)
* (44x - 3161) / 35 = √((x - 88)² + 4356)
* Square both sides again:
* (44x - 3161)² / 35² = (x - 88)² + 4356
* (1936x² - 278128x + 9992081) / 1225 = x² - 176x + 7744 + 4356
* (1936x² - 278128x + 9992081) / 1225 = x² - 176x + 12100
* 1936x² - 278128x + 9992081 = 1225(x² - 176x + 12100)
* 1936x² - 278128x + 9992081 = 1225x² - 215600x + 14822500
* 711x² - 62528x - 4830419 = 0
* Solve the quadratic equation using the quadratic formula:
* x = (62528 ± √(62528² - 4 * 711 * (-4830419))) / (2 * 711)
* x = (62528 ± √(3909775384 + 13739773956)) / 1422
* x = (62528 ± √17649549340) / 1422
* x = (62528 ± 132851.61) / 1422
* x ≈ 136.69 or x ≈ -48.68
* Since the plane is traveling east, we choose the positive solution.
* x ≈ 136.69
6. **Position of the Plane:**
* The plane's position is approximately (136.69, 66).
* This means the plane is approximately 136.69 miles east of station B.
**Final Answer**
The plane is approximately 136.69 miles east of station B.
Question 1169035: A satellite dish has a shape called paraboloid so that its cross-sections through its center (lowest point) are parabolas, all having the same focus. Radio signals sent to it bounce off the surface and are reflected to the focus. The receiver is then placed at the focus. If the satellite dish is 3 meters across and 0.625 meters deep at its center, how far should the receiver be from the center. solution please
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1169034: A satellite dish has a shape called paraboloid so that its cross-sections through its center (lowest point) are parabolas, all having the same focus. Radio signals sent to it bounce off the surface and are reflected to the focus. The receiver is then placed at the focus. If the satellite dish is 3 meters across and 0.625 meters deep at its center, how far should the receiver be from the center. solution please
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1170335: Find the length of the latus rectum and the equation of the parabola with vertex at the origin, directrix x=-3 and focus (3, 0). Sketch the graph.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step.
**1. Determine the Orientation of the Parabola:**
* The vertex is at the origin (0, 0).
* The focus is at (3, 0).
* The directrix is x = -3.
* Since the focus is to the right of the vertex and the directrix is to the left, the parabola opens to the right.
**2. Determine the Value of 'p':**
* The distance between the vertex and the focus is 'p'.
* The distance between the vertex (0, 0) and the focus (3, 0) is 3.
* Therefore, p = 3.
**3. Find the Equation of the Parabola:**
* Since the parabola opens to the right and the vertex is at the origin, the equation is of the form:
$y^2 = 4px$
* Substitute p = 3 into the equation:
$y^2 = 4(3)x$
$y^2 = 12x$
**4. Find the Length of the Latus Rectum:**
* The length of the latus rectum is 4p.
* Since p = 3, the length of the latus rectum is 4(3) = 12.
**5. Sketch the Graph:**
* **Vertex:** (0, 0)
* **Focus:** (3, 0)
* **Directrix:** x = -3
* **Latus Rectum:** The latus rectum passes through the focus and is perpendicular to the axis of symmetry. Its endpoints are at a distance of 2p from the focus.
* Since 2p = 6, the endpoints of the latus rectum are at (3, 6) and (3, -6).
**Graph:**
```
^ y-axis
|
6 | * (3, 6)
| /
| /
| /
| /
0 +-----------+---> x-axis
| \
| \
| \
-6 | * (3, -6)
|
-3 | Directrix x=-3
```
**Summary:**
* **Length of the Latus Rectum:** 12
* **Equation of the Parabola:** $y^2 = 12x$
Question 1170336: Find the focus, directrix, and equation of the parabola with vertex at the origin, axis along y-axis; opening upward; and the length of the latus rectum is 12. Sketch the graph.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step.
**1. Equation of the Parabola:**
* Since the vertex is at the origin (0, 0), the axis is along the y-axis, and the parabola opens upward, the equation of the parabola is of the form:
$x^2 = 4py$
where $p > 0$.
**2. Length of the Latus Rectum:**
* The length of the latus rectum is given as 12.
* The length of the latus rectum is also equal to $4p$.
* Therefore, $4p = 12$.
* Solving for $p$:
$p = \frac{12}{4} = 3$
**3. Equation of the Parabola (Specific):**
* Substitute $p = 3$ into the equation $x^2 = 4py$:
$x^2 = 4(3)y$
$x^2 = 12y$
**4. Focus:**
* The focus of the parabola is at (0, p).
* Since $p = 3$, the focus is at (0, 3).
**5. Directrix:**
* The directrix is a horizontal line given by the equation $y = -p$.
* Since $p = 3$, the directrix is $y = -3$.
**6. Sketch the Graph:**
* **Vertex:** (0, 0)
* **Focus:** (0, 3)
* **Directrix:** y = -3
* **Latus Rectum:** The latus rectum passes through the focus and is perpendicular to the axis of symmetry. Its endpoints are at a distance of $2p$ from the focus.
* Since $2p = 6$, the endpoints of the latus rectum are at (-6, 3) and (6, 3).
**Graph:**
```
^ y-axis
|
|
3 | * (0, 3) - Focus
| / \
| / \
|/ \
0 +-----------+---> x-axis
|\ /|
| \ / |
| \ / |
-3 | v - Directrix
|
```
**Summary:**
* **Equation of the Parabola:** $x^2 = 12y$
* **Focus:** (0, 3)
* **Directrix:** $y = -3$
Question 1206901: The sides of a nuclear power plant cooling tower form a hyperbola. The diameter of the bottom of the tower is 288 feet. The smallest diameter of the tower is 143 feet which is 393.5 feet above the ground. The tower is 581 feet tall.
Find the width of the tower at a height of 38 feet.
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The sides of a nuclear power plant cooling tower form a hyperbola.
The diameter of the bottom of the tower is 288 feet.
The smallest diameter of the tower is 143 feet which is 393.5 feet above the ground.
The tower is 581 feet tall.
Find the width of the tower at a height of 38 feet.
~~~~~~~~~~~~~~~~~~~~~~~~~~
The solution in the post by @CPhill is TOTALLY and FATALLY WRONG.
The expected hyperbola in this problem is horizontal, with horizontal transverse axis.
In the post by @CPhill, the hyperbola is vertical, with vertical transverse axis.
His initial hypothesis about the form of the hyperbola for this problem is  and and  . .
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\
Regarding the post by @CPhill . . .
Keep in mind that @CPhill is a pseudonym for the Google artificial intelligence.
The artificial intelligence is like a baby now. It is in the experimental stage
of development and can make mistakes and produce nonsense without any embarrassment.
It has no feeling of shame - it is shameless.
This time, again, it made an error.
Although the @CPhill' solution are copy-paste Google AI solutions, there is one essential difference.
Every time, Google AI makes a note at the end of its solutions that Google AI is experimental
and can make errors/mistakes.
All @CPhill' solutions are copy-paste of Google AI solutions, with one difference:
@PChill never makes this notice and never says that his solutions are copy-past that of Google.
So, he NEVER SAYS TRUTH.
Every time, @CPhill embarrassed to tell the truth.
But I am not embarrassing to tell the truth, as it is my duty at this forum.
And the last my comment.
When you obtain such posts from @CPhill, remember, that NOBODY is responsible for their correctness,
until the specialists and experts will check and confirm their correctness.
Without it, their reliability is ZERO and their creadability is ZERO, too.
Question 1170522: The cable of suspension bridge hangs in the shape of a parabola. The towers supporting the cable are 400ft apart and 150ft high. If the cable, at its lowest, is 30ft above the bridge at its midpoint, how high is the cable 50ft away (horizontally) from either tower?
Found 3 solutions by Edwin McCravy, ikleyn, CPhill:
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
You can put this solution on YOUR website!
As we see, AI is getting better. One day it'll beat us all. I read that it has
been a long time since a human master chess champion was able to beat an AI
computer program programmed to learn from its mistakes.
I just asked AI about that, and got this answer:
AI:
The last time a human world chess champion was able to beat a chess program
designed to learn from its mistakes in a formal match was in 1996, during the
first match between Garry Kasparov and IBM's Deep Blue.
In that match:
Kasparov lost the first game but ultimately won the six-game match 4 - 2. This
victory demonstrated that, while computers were becoming formidable opponents,
humans could still prevail at the highest level of chess.
However, the following year, in 1997, Deep Blue was upgraded and defeated
Kasparov in a highly publicized rematch with a score of 3.5 - 2.5. This marked the
first time a reigning world champion lost a match to a computer under standard
tournament conditions.
Since then, chess engines have continued to improve dramatically, with modern
programs like Stockfish, AlphaZero, and Leela Chess Zero outperforming even the
strongest human players. Today, no human can consistently defeat top chess
engines, which are now considered far superior in both calculation and strategic
understanding.
EM
My question now is: When are we humans going to stop electing selfish multi-
billionaire humans as presidents of countries, as in the present USA, and start
electing AI?
Edwin
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The cable of suspension bridge hangs in the shape of a parabola.
The towers supporting the cable are 400 ft apart and 150 ft high.
If the cable, at its lowest is 30 ft above the bridge at its midpoint,
how high is the cable 50 ft away (horizontally) from either tower?
~~~~~~~~~~~~~~~~~~~~~~~~~
If we place the origin of the coordinate system at the bridge level midpoint
between the two towers, we have the vertex of the parabola at the point (0,30).
So, we write an equation of the parabola in vertex form
y = ax^2 + 30.
Coefficient "a" is unknown. It is the only unknown in this problem now.
To find it, we use the condition at the endpoint: y= 150 at x= 400/2 = 200. It gives
150 = a*200^2 + 30
150 - 30 = a*40000
120 = 40000a
a =  = = 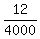 = = 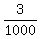 .
Thus the parabola is y = .
Thus the parabola is y = 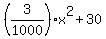 .
To find the level of the cable at 50 ft from the tower, we substitute x = 200-50 = 150 ft
into the equation of the parabola.
This way we get the height of the cable at the point x= 150 ft, which is 50 feet from the tower
y = .
To find the level of the cable at 50 ft from the tower, we substitute x = 200-50 = 150 ft
into the equation of the parabola.
This way we get the height of the cable at the point x= 150 ft, which is 50 feet from the tower
y = 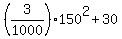 = 97.5 ft. ANSWER = 97.5 ft. ANSWER
Solved.
//////////////////
It can be solved mentally, without using equations, too.
The maximum difference of the levels of the cable is 150 - 30 = 120 ft.
The distance 150 ft from the central point to the tower is 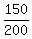 = =  of the half the bridge length.
Hence, the level of the cable at x= 150 ft from the center is
30 +
of the half the bridge length.
Hence, the level of the cable at x= 150 ft from the center is
30 + 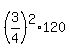 = 30 + = 30 + 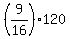 = 30 + = 30 + 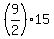 = 30 + 9*7.5 = use your calculator = 97.5 ft,
giving the same answer. = 30 + 9*7.5 = use your calculator = 97.5 ft,
giving the same answer.
///////////////////////////////////
Edwin, regarding your lamentations, don't you think that this AI would have been paid
by the same multi-billionaires (or trillionairs) and you will ELECT it as a highest ruler, without even suspecting it ?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**1. Set up a Coordinate System**
* Place the vertex of the parabola (the lowest point of the cable) at the origin (0, 30).
* The towers are 400 feet apart, so they are located at (-200, 150) and (200, 150).
**2. Find the Equation of the Parabola**
* The general equation of a parabola with a vertical axis of symmetry and vertex (h, k) is:
(x - h)^2 = 4p(y - k)
* In our case, the vertex is (0, 30), so the equation becomes:
x^2 = 4p(y - 30)
* We know the towers are at (200, 150). Plug these coordinates into the equation to find 'p':
(200)^2 = 4p(150 - 30)
40000 = 4p(120)
40000 = 480p
p = 40000 / 480 = 83.333... = 250/3
* Now, plug 'p' back into the equation:
x^2 = 4(250/3)(y - 30)
x^2 = (1000/3)(y - 30)
**3. Find the Height 50 Feet from a Tower**
* We want to find the height of the cable 50 feet horizontally from either tower. Since the towers are at x = ±200, we're looking for the height at x = 200 - 50 = 150 and x = -200 + 50 = -150. Due to symmetry, the height will be the same.
* Plug x = 150 (or x = -150) into the parabola equation:
(150)^2 = (1000/3)(y - 30)
22500 = (1000/3)(y - 30)
22500 * (3/1000) = y - 30
67.5 = y - 30
y = 67.5 + 30
y = 97.5
**4. Answer**
* The cable is 97.5 feet high 50 feet away (horizontally) from either tower.
**Final Answer:** 97.5 feet
Question 1170527: LORAN navigational transmitters A and B are located at (-130,0) and (130,0) respectively. A receiver P on a fishing boat somewhere in the first quadrant listens to the pair (A,B) of the transmissions and computes the difference of the distance from boat A and B as 240 miles. Find the equation of the hyperbola on P is located.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let A = (-130, 0) and B = (130, 0). Let P = (x, y) be the position of the fishing boat.
The distance from P to A is $d_A = \sqrt{(x - (-130))^2 + (y - 0)^2} = \sqrt{(x + 130)^2 + y^2}$.
The distance from P to B is $d_B = \sqrt{(x - 130)^2 + (y - 0)^2} = \sqrt{(x - 130)^2 + y^2}$.
We are given that the difference in distances is 240 miles, i.e., $|d_A - d_B| = 240$. Since P is in the first quadrant, we can assume $d_A > d_B$, so $d_A - d_B = 240$.
Thus, $\sqrt{(x + 130)^2 + y^2} - \sqrt{(x - 130)^2 + y^2} = 240$.
We need to find the equation of the hyperbola.
First, rearrange the equation:
$\sqrt{(x + 130)^2 + y^2} = \sqrt{(x - 130)^2 + y^2} + 240$
Square both sides:
$(x + 130)^2 + y^2 = (x - 130)^2 + y^2 + 480\sqrt{(x - 130)^2 + y^2} + 240^2$
$x^2 + 260x + 130^2 + y^2 = x^2 - 260x + 130^2 + y^2 + 480\sqrt{(x - 130)^2 + y^2} + 57600$
$520x - 57600 = 480\sqrt{(x - 130)^2 + y^2}$
Divide by 80:
$6.5x - 720 = 6\sqrt{(x - 130)^2 + y^2}$
Square both sides again:
$(6.5x - 720)^2 = 36[(x - 130)^2 + y^2]$
$42.25x^2 - 9360x + 518400 = 36(x^2 - 260x + 16900 + y^2)$
$42.25x^2 - 9360x + 518400 = 36x^2 - 9360x + 608400 + 36y^2$
$6.25x^2 - 36y^2 = 90000$
Divide by 90000:
$\frac{6.25x^2}{90000} - \frac{36y^2}{90000} = 1$
$\frac{x^2}{14400} - \frac{y^2}{2500} = 1$
$\frac{x^2}{120^2} - \frac{y^2}{50^2} = 1$
Therefore, the equation of the hyperbola is $\frac{x^2}{14400} - \frac{y^2}{2500} = 1$.
Final Answer: The final answer is $\boxed{\frac{x^2}{14400}-\frac{y^2}{2500}=1}$
Question 1170538: A satellite dish is shaped like a paraboloid, with the receiver placed at the focus. It is to have a depth of 0.44 m at the vertex, with the receiver placed 0.11 m away from the vertex. What should the diameter of
the satellite dish be?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the paraboloid be represented by the equation $x^2 = 4py$, where the vertex is at the origin (0, 0) and the focus is at (0, p).
We are given that the receiver is placed 0.11 m away from the vertex, which means the focus is at (0, 0.11). Therefore, p = 0.11 m.
The equation of the paraboloid is $x^2 = 4(0.11)y$, or $x^2 = 0.44y$.
The depth of the dish is 0.44 m, which means when y = 0.44 m, we can find the x-coordinate of the edge of the dish.
Substitute y = 0.44 into the equation:
$x^2 = 0.44(0.44) = 0.1936$
$x = \pm \sqrt{0.1936} = \pm 0.44$
The diameter of the dish is the distance between the two x-coordinates, which is:
Diameter = 0.44 - (-0.44) = 2(0.44) = 0.88 m.
Therefore, the diameter of the satellite dish should be 0.88 m.
Final Answer: The final answer is $\boxed{0.88}$
Question 1170539: A satellite dish is shaped like a paraboloid, with the receiver placed at the focus. It is to have a depth of 0.44 m at the vertex, with the receiver placed 0.11 m away from the vertex. What should the diameter of the satellite dish be?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the paraboloid be represented by the equation $x^2 = 4py$, where the vertex is at the origin (0, 0) and the focus is at (0, p).
We are given that the receiver is placed 0.11 m away from the vertex, which means the focus is at (0, 0.11). Therefore, p = 0.11 m.
The equation of the paraboloid is $x^2 = 4(0.11)y$, or $x^2 = 0.44y$.
The depth of the dish is 0.44 m, which means when y = 0.44 m, we can find the x-coordinate of the edge of the dish.
Substitute y = 0.44 into the equation:
$x^2 = 0.44(0.44) = 0.1936$
$x = \pm \sqrt{0.1936} = \pm 0.44$
The diameter of the dish is the distance between the two x-coordinates, which is:
Diameter = 0.44 - (-0.44) = 2(0.44) = 0.88 m.
Therefore, the diameter of the satellite dish should be 0.88 m.
Final Answer: The final answer is $\boxed{0.88}$
Question 1170541: Two stations, located at M(−1.5,0) and N(1.5,0)(units are in km), simultaneously send sound signals to a ship, with the signal traveling at the speed of 0.33 km/s. If the signal from N was received by the ship four seconds before the signal it received from M, find the equation of the curve containing the possible location of the ship.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the ship's location be (x, y).
The distance between the ship and station M is $d_M = \sqrt{(x + 1.5)^2 + y^2}$.
The distance between the ship and station N is $d_N = \sqrt{(x - 1.5)^2 + y^2}$.
The time it takes for the signal from M to reach the ship is $t_M = \frac{d_M}{0.33}$.
The time it takes for the signal from N to reach the ship is $t_N = \frac{d_N}{0.33}$.
We are given that the signal from N was received 4 seconds before the signal from M. This means $t_M - t_N = 4$.
Substituting the expressions for $t_M$ and $t_N$, we get:
$$\frac{d_M}{0.33} - \frac{d_N}{0.33} = 4$$
$$d_M - d_N = 4(0.33) = 1.32$$
$$\sqrt{(x + 1.5)^2 + y^2} - \sqrt{(x - 1.5)^2 + y^2} = 1.32$$
Now, we need to eliminate the square roots.
$$\sqrt{(x + 1.5)^2 + y^2} = \sqrt{(x - 1.5)^2 + y^2} + 1.32$$
Square both sides:
$$(x + 1.5)^2 + y^2 = (x - 1.5)^2 + y^2 + 2(1.32)\sqrt{(x - 1.5)^2 + y^2} + (1.32)^2$$
$$x^2 + 3x + 2.25 + y^2 = x^2 - 3x + 2.25 + y^2 + 2.64\sqrt{(x - 1.5)^2 + y^2} + 1.7424$$
$$6x - 1.7424 = 2.64\sqrt{(x - 1.5)^2 + y^2}$$
Divide by 2.64:
$$\frac{6x - 1.7424}{2.64} = \sqrt{(x - 1.5)^2 + y^2}$$
$$\frac{600x - 174.24}{264} = \sqrt{(x - 1.5)^2 + y^2}$$
$$\frac{250x - 72.6}{110} = \sqrt{(x - 1.5)^2 + y^2}$$
$$\frac{125x - 36.3}{55} = \sqrt{(x - 1.5)^2 + y^2}$$
Square both sides again:
$$\left(\frac{125x - 36.3}{55}\right)^2 = (x - 1.5)^2 + y^2$$
$$\frac{(125x - 36.3)^2}{55^2} = (x - 1.5)^2 + y^2$$
$$\frac{15625x^2 - 9075x + 1317.69}{3025} = x^2 - 3x + 2.25 + y^2$$
$$15625x^2 - 9075x + 1317.69 = 3025x^2 - 9075x + 6806.25 + 3025y^2$$
$$12600x^2 - 3025y^2 = 5488.56$$
Divide by 5488.56:
$$\frac{12600x^2}{5488.56} - \frac{3025y^2}{5488.56} = 1$$
$$\frac{x^2}{0.4356} - \frac{y^2}{1.8144} = 1$$
$$\frac{x^2}{(0.66)^2} - \frac{y^2}{(1.347)^2} = 1$$
The equation of the curve is a hyperbola.
Final Answer: The final answer is $\boxed{\frac{x^2}{0.4356}-\frac{y^2}{1.8144}=1}$
Question 1170507: For an object in an elliptical orbit around the moon, the points in the orbit that are closest to and farthest from the center of the moon are called perilune and apolune, respectively. These are the vertices of the orbit. The center of the moon is at one focus of the orbit. A spacecraft was placed in a lunar orbit with perilune at a = 89 mi and apolune at b = 258 mi above the surface of the moon. Assuming that the moon is a sphere of radius 1075 mi, find an equation for the orbit of this spacecraft. (Place the coordinate axes so that the origin is at the center of the orbit and the foci are located on the x-axis. Round each answer to the nearest whole number.)
x2 + y2 = 1
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1170844: I have a parabola with a length of 72 feet and a height of 64 ft, the goal is to find the vertex as well as the x-intercepts and then write the parabola in standard, vertex and factored form; thanks a ton!
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step by step.
**1. Set up a Coordinate System**
To make the calculations easier, let's place the parabola in a coordinate system. We'll place the vertex on the y-axis, which will simplify the equations.
* Let the vertex be at (0, 64).
* The parabola opens downwards since it has a maximum height of 64 ft.
* The length of 72 feet means the x-intercepts are at (-36, 0) and (36, 0).
**2. Vertex Form**
The vertex form of a parabola is:
y = a(x - h)² + k
where (h, k) is the vertex.
* We know the vertex is (0, 64), so h = 0 and k = 64.
* y = a(x - 0)² + 64
* y = ax² + 64
**3. Find the Value of 'a'**
We can use one of the x-intercepts to find 'a'. Let's use (36, 0):
* 0 = a(36)² + 64
* 0 = 1296a + 64
* -64 = 1296a
* a = -64 / 1296
* a = -1 / 20.25
* a = -4 / 81
Therefore, the vertex form is:
y = (-4/81)x² + 64
**4. Standard Form**
The standard form of a parabola is:
y = ax² + bx + c
We already have the vertex form:
y = (-4/81)x² + 64
Since there's no 'x' term, b = 0. So the standard form is:
y = (-4/81)x² + 64
**5. Factored Form**
The factored form of a parabola is:
y = a(x - r₁)(x - r₂)
where r₁ and r₂ are the x-intercepts.
* We know the x-intercepts are (-36, 0) and (36, 0), so r₁ = -36 and r₂ = 36.
* We know a = -4/81.
Therefore, the factored form is:
y = (-4/81)(x - (-36))(x - 36)
y = (-4/81)(x + 36)(x - 36)
**Summary**
* **Vertex:** (0, 64)
* **X-intercepts:** (-36, 0) and (36, 0)
* **Vertex Form:** y = (-4/81)x² + 64
* **Standard Form:** y = (-4/81)x² + 64
* **Factored Form:** y = (-4/81)(x + 36)(x - 36)
Question 1209900: Let $x$ and $y$ be real numbers such that
x^2 + 3xy + 2y^2 = 1 - 12x + 5y.
Find all possible values of x + y. Enter your answer using interval notation.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let the given equation be
$$x^2 + 3xy + 2y^2 = 1 - 12x + 5y$$
We can factor the left side as
$$(x+y)(x+2y) = 1 - 12x + 5y$$
Let $u = x+y$ and $v = x+2y$. Then $u+y=x+y$ so $y = v-u$ and $x = u-y = u-(v-u) = 2u-v$.
Substituting into the given equation, we have
$$uv = 1 - 12(2u-v) + 5(v-u)$$
$$uv = 1 - 24u + 12v + 5v - 5u$$
$$uv = 1 - 29u + 17v$$
$$uv - 17v = 1 - 29u$$
$$v(u-17) = 1 - 29u$$
If $u \neq 17$, we can solve for $v$:
$$v = \frac{1-29u}{u-17}$$
Then $y = v-u = \frac{1-29u}{u-17} - u = \frac{1-29u-u(u-17)}{u-17} = \frac{1-29u-u^2+17u}{u-17} = \frac{-u^2-12u+1}{u-17}$
And $x = 2u-v = 2u - \frac{1-29u}{u-17} = \frac{2u(u-17)-(1-29u)}{u-17} = \frac{2u^2-34u-1+29u}{u-17} = \frac{2u^2-5u-1}{u-17}$
Since $x$ and $y$ are real numbers, we must have $u \neq 17$.
We are interested in the possible values of $u = x+y$.
The equation can be rewritten as
$$x^2 + 3xy + 2y^2 + 12x - 5y - 1 = 0$$
Consider this as a quadratic in $x$:
$$x^2 + (3y+12)x + (2y^2-5y-1) = 0$$
For $x$ to be real, the discriminant must be non-negative:
$$(3y+12)^2 - 4(2y^2-5y-1) \ge 0$$
$$9y^2 + 72y + 144 - 8y^2 + 20y + 4 \ge 0$$
$$y^2 + 92y + 148 \ge 0$$
The roots of $y^2 + 92y + 148 = 0$ are
$$y = \frac{-92 \pm \sqrt{92^2 - 4(148)}}{2} = \frac{-92 \pm \sqrt{8464 - 592}}{2} = \frac{-92 \pm \sqrt{7872}}{2} = -46 \pm \sqrt{1968}$$
$$y = -46 \pm 4\sqrt{123}$$
Thus $y \le -46 - 4\sqrt{123}$ or $y \ge -46 + 4\sqrt{123}$.
Consider the equation as a quadratic in $y$:
$$2y^2 + (3x-5)y + (x^2+12x-1) = 0$$
The discriminant must be non-negative:
$$(3x-5)^2 - 4(2)(x^2+12x-1) \ge 0$$
$$9x^2 - 30x + 25 - 8x^2 - 96x + 8 \ge 0$$
$$x^2 - 126x + 33 \ge 0$$
The roots of $x^2 - 126x + 33 = 0$ are
$$x = \frac{126 \pm \sqrt{126^2 - 4(33)}}{2} = \frac{126 \pm \sqrt{15876 - 132}}{2} = \frac{126 \pm \sqrt{15744}}{2} = 63 \pm \sqrt{3936}$$
Thus $x \le 63 - \sqrt{3936}$ or $x \ge 63 + \sqrt{3936}$.
If $u=17$, then $0=1-29(17)=-492$, which is impossible. So $u\ne 17$ for all real solutions.
We need to find the range of $u$.
Let $y=ax+b$.
Then $x^2+3x(ax+b)+2(ax+b)^2=1-12x+5(ax+b)$.
$x^2+3ax^2+3bx+2a^2x^2+4abx+2b^2=1-12x+5ax+5b$.
$(1+3a+2a^2)x^2+(3b+4ab+12-5a)x+2b^2-5b-1=0$.
For real solutions, the discriminant must be non-negative.
$(3b+4ab+12-5a)^2-4(1+3a+2a^2)(2b^2-5b-1)\ge 0$.
$u=x+y=x+ax+b=(1+a)x+b$.
We want to find $u$.
If $x+y=17$, then $v=\frac{1-29(17)}{17-17}$. This is impossible.
We have $u=x+y$. Let $x+y=c$ and $x=c-y$.
$(c-y)^2+3(c-y)y+2y^2=1-12(c-y)+5y$.
$c^2-2cy+y^2+3cy-3y^2+2y^2=1-12c+12y+5y$.
$c^2+cy=1-12c+17y$.
$y(c-17)=c^2+12c-1$.
$y=\frac{c^2+12c-1}{c-17}$.
$x=c-y = c-\frac{c^2+12c-1}{c-17} = \frac{c(c-17)-c^2-12c+1}{c-17} = \frac{-29c+1}{c-17}$.
For real $x$ and $y$, $c\ne 17$.
Therefore $x+y$ can be any real number except 17.
Final Answer: The final answer is $\boxed{(-\infty,17)\cup(17,\infty)}$
Question 1171137: Navigational transmitters Q and R are located at (-130,0) and (130,0) respectively. A receiver A on a fishing boat somewhere in the first quadrant listens to pair (Q,R) of the transmissions and computes the difference of the distance from boat Q and R as 240 miles. What is the equation of the hyperbola on which A is located?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's break down this problem step-by-step.
**Understanding the Hyperbola**
The key information is that the difference of the distances from the receiver A to the transmitters Q and R is constant (240 miles). This defines a hyperbola.
**Given Information:**
* Transmitter Q: (-130, 0)
* Transmitter R: (130, 0)
* Difference in distances: |AQ - AR| = 240 miles
* Receiver A is in the first quadrant.
**Hyperbola Equation**
The standard equation of a hyperbola with horizontal transverse axis and center at the origin is:
$$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$$
Where:
* 2a is the difference of the distances from any point on the hyperbola to the foci.
* The foci are at (±c, 0).
* c is the distance from the center to each focus.
* b^2 = c^2 - a^2
**Finding the Parameters**
1. **2a:** The difference in distances is 240 miles, so 2a = 240, which means a = 120.
2. **c:** The foci are at (-130, 0) and (130, 0), so c = 130.
3. **b^2:** We can find b^2 using the relationship b^2 = c^2 - a^2:
* b^2 = 130^2 - 120^2 = 16900 - 14400 = 2500
**Writing the Equation**
Now, we can substitute the values of a^2 and b^2 into the hyperbola equation:
$$\frac{x^2}{120^2} - \frac{y^2}{2500} = 1$$
$$\frac{x^2}{14400} - \frac{y^2}{2500} = 1$$
**Therefore, the equation of the hyperbola on which A is located is:**
$$\frac{x^2}{14400} - \frac{y^2}{2500} = 1$$
Question 1170862: An endpoint of the minor axis is at (-1, -10), a vertex is at (-14, 2) and a focus is at (4, 2)
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
An endpoint of the minor axis is at (-1, -10), a vertex is at (-14, 2) and a focus is at (4, 2)
~~~~~~~~~~~~~~~~~~~~~~~~~~
Very good.
What do you want to get from tutors ?
Question 1171519: An arch of a bridge over a highway is semi-elliptical in shape and 50 feet across. The highest point of the arch is 15 feet above the highway. What is the maximum height of a vehicle 10 feet wide that can fit under arch ?
Answer by ikleyn(52778)   (Show Source): (Show Source):
Question 1172679: The following application was developed during World War II. It shows how the properties of hyperbolas can be used in radar and other detection systems.
Two microphones, 1 mile apart, record an explosion. Microphone A receives the sound 2 seconds before microphone B. Where did the explosion occur? (assume sound travels at 1100 feet per second.
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Absolutely, let's solve this problem using the properties of hyperbolas.
**Understanding the Problem**
* **Hyperbola Property:** A hyperbola is defined as the set of all points where the difference of the distances to two fixed points (foci) is constant.
* **Microphones as Foci:** In this case, the microphones A and B are the foci of the hyperbola.
* **Time Difference:** The 2-second difference in sound arrival times indicates a constant difference in distances from the explosion to the microphones.
* **Sound Speed:** We'll use the speed of sound to convert the time difference into a distance difference.
**Solving the Problem**
1. **Convert Miles to Feet:**
* 1 mile = 5280 feet
2. **Calculate Distance Difference:**
* Distance difference = (time difference) * (speed of sound)
* Distance difference = 2 seconds * 1100 feet/second = 2200 feet
3. **Hyperbola Parameters:**
* The distance between the foci (2c) is 5280 feet.
* Therefore, c = 2640 feet.
* The constant distance difference (2a) is 2200 feet.
* Therefore, a = 1100 feet.
4. **Finding b:**
* We use the relationship c^2 = a^2 + b^2
* b^2 = c^2 - a^2
* b^2 = (2640)^2 - (1100)^2
* b^2 = 6969600 - 1210000
* b^2 = 5759600
* b = sqrt(5759600)
* b = approximately 2400 feet.
5. **Hyperbola Equation:**
* We can set up a coordinate system where the microphones are on the x-axis, with the midpoint between them as the origin.
* The equation of the hyperbola is (x^2 / a^2) - (y^2 / b^2) = 1
* (x^2/1100^2) - (y^2/2400^2) = 1
* (x^2/1210000) - (y^2/5760000) = 1
6. **Determining the Location:**
* The explosion occurred somewhere on the branch of the hyperbola that is closer to microphone A, because A received the sound first.
* Because we do not have any further information, we cannot specify the exact x and y coordinate. We do know the explosion occured on a hyperbola, that has the equation calculated above. We also know that the branch of the hyperbola that is closer to microphone A is the branch that contains the explosion.
**Conclusion**
The explosion occurred on a branch of the hyperbola defined by the equation (x^2 / 1210000) - (y^2 / 5760000) = 1, closer to microphone A. Without additional information, we can't pinpoint the exact coordinates.
Question 1174416: A 10-feet tall, 10-feet wide truck is approaching a tunnel on a one-way road. The arch at the tunnel’s
entrance forms the upper half of an ellipse with a height of 15 feet at the center and a base of 12 feet wide.
Consider that the center is at the origin, will the truck be able to fit through the arch?
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's analyze the ellipse describing the tunnel's entrance.
**1. Equation of the Ellipse:**
* The ellipse has a horizontal major axis (base of 12 feet) and a vertical minor axis (height of 15 feet).
* The center is at the origin (0, 0).
* The semi-major axis (horizontal) is a = 12 / 2 = 6 feet.
* The semi-minor axis (vertical) is b = 15 feet.
* The equation of the ellipse is: (x^2 / a^2) + (y^2 / b^2) = 1
* Substituting the values of a and b: (x^2 / 36) + (y^2 / 225) = 1
**2. Truck Dimensions:**
* Truck height: 10 feet
* Truck width: 10 feet
**3. Checking if the Truck Fits:**
* Since the truck is 10 feet wide, we need to check the tunnel's height at x = 10 / 2 = 5 feet (half the truck's width).
* Plug x = 5 into the ellipse equation and solve for y:
* (5^2 / 36) + (y^2 / 225) = 1
* (25 / 36) + (y^2 / 225) = 1
* (y^2 / 225) = 1 - (25 / 36) = (36 - 25) / 36 = 11 / 36
* y^2 = 225 * (11 / 36)
* y = sqrt(225 * 11 / 36) = (15 / 6) * sqrt(11) = (5 / 2) * sqrt(11)
* y ≈ (5 / 2) * 3.3166 ≈ 8.2915 feet
* Since the tunnel is only the upper half of the ellipse, we keep the positive value of y.
* The tunnel's height at 5 feet from the center is approximately 8.2915 feet.
**4. Comparing Heights:**
* The truck is 10 feet tall.
* The tunnel's height at 5 feet from the center is about 8.2915 feet.
* Since 10 feet > 8.2915 feet, the truck is taller than the tunnel at the edges of the truck.
* Therefore, the truck will not fit through the arch.
**Conclusion:**
The truck will not be able to fit through the arch.
Question 1174826: find the equation of parabola which has contact of third order with the conic ax^2 +2hxy + by^2 +2gx +2fy +c =0 at origin.
Found 2 solutions by ikleyn, CPhill:
Answer by ikleyn(52778)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The solution in the post by @CPhill is incorrect.
It is incorrect TWO TIMES due to two reasons.
(1) The equation of the parabola is written in incorrect form.
(2) in the solution, @CPhill makes an assumption that the tangent is along x-axis.
The problem nowhere says it, so this assumption is WRONG and irrelevant to the problem.
To be correct, this assumption should not be made.
Google AI gives another solution to this problem (quite long) without making wrong assumptions.
See the link
https://www.google.com/search?q=find+the+equation+of+parabola+which+has+contact+of+third+order+with+the+conic+ax%5E2+%2B2hxy+%2B+by%5E2+%2B2gx+%2B2fy+%2Bc+%3D0+at+origin.&rlz=1C1CHBF_enUS1071US1071&oq=find+the+equation+of+parabola+which+has+contact+of+third+order+with+the+conic+ax%5E2+%2B2hxy+%2B+by%5E2+%2B2gx+%2B2fy+%2Bc+%3D0+at+origin.&gs_lcrp=EgZjaHJvbWUyBggAEEUYOdIBCTE5NTFqMGoxNagCCLACAfEFU-UGEVhaVo0&sourceid=chrome&ie=UTF-8
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let's solve this problem step-by-step.
**1. Understand Contact of Third Order**
* Two curves have contact of third order at a point if they have the same value, the same first derivative, the same second derivative, and the same third derivative at that point.
**2. Parabola Equation**
* Since the parabola has contact at the origin, and we need a general form, we'll use the form:
* y = Ax² + Bx³
* Note that the parabola must pass through the origin (0,0) and the tangent at the origin must be along the x axis.
**3. Conic Equation**
* The given conic is:
* ax² + 2hxy + by² + 2gx + 2fy + c = 0
**4. Contact at the Origin**
* Since both curves pass through the origin (0, 0), we have c = 0.
* Thus the conic equation becomes:
* ax² + 2hxy + by² + 2gx + 2fy = 0
**5. Derivatives**
* **Parabola:**
* y = Ax² + Bx³
* y' = 2Ax + 3Bx²
* y'' = 2A + 6Bx
* y''' = 6B
* **Conic:**
* To find derivatives, we'll use implicit differentiation.
* ax² + 2hxy + by² + 2gx + 2fy = 0
* Differentiate w.r.t x: 2ax + 2hy + 2hx y' + 2by y' + 2g + 2fy' = 0
* At (0, 0): 2g + 2fy' = 0 => y' = -g/f
* If the tangent is along the x axis then y' = 0, thus g = 0.
* Conic equation now is: ax² + 2hxy + by² + 2fy = 0.
* 2ax + 2hy + 2hxy' + 2byy' + 2fy'=0.
* Differentiate again. 2a + 2hy' + 2hy' + 2hxy'' + 2by'y' + 2byy'' + 2fy'' = 0.
* At (0,0) with g=0 and y'=0, 2a + 2fy''=0, thus y'' = -a/f
* Differentiate again. 2hy'' + 2hy'' + 2hy'' + 2hxy''' + 4by'y'' + 2by'y'' + 2byy''' + 2fy''' = 0
* At (0,0) with g=0 and y'=0, 6hy'' + 2fy''' = 0, thus y''' = -3hy''/f = 3ha/f².
**6. Equate Derivatives at (0, 0)**
* **y'(0):**
* Parabola: 0
* Conic: 0 (since g=0)
* **y''(0):**
* Parabola: 2A
* Conic: -a/f
* Therefore, 2A = -a/f => A = -a/(2f)
* **y'''(0):**
* Parabola: 6B
* Conic: 3ha/f²
* Therefore, 6B = 3ha/f² => B = ha/(2f²)
**7. Parabola Equation**
* Substitute A and B into the parabola equation:
* y = (-a/(2f))x² + (ha/(2f²))x³
* y = (-ax²f + hax³)/(2f²)
* 2f²y = -ax²f + hax³
* 2f²y + ax²f - hax³ = 0
**Final Equation**
The equation of the parabola is:
**2f²y + ax²f - hax³ = 0**
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420, 3421..3465, 3466..3510, 3511..3555, 3556..3600, 3601..3645, 3646..3690, 3691..3735, 3736..3780, 3781..3825, 3826..3870, 3871..3915, 3916..3960, 3961..4005, 4006..4050, 4051..4095, 4096..4140, 4141..4185, 4186..4230, 4231..4275, 4276..4320, 4321..4365, 4366..4410, 4411..4455, 4456..4500, 4501..4545, 4546..4590, 4591..4635, 4636..4680, 4681..4725, 4726..4770, 4771..4815, 4816..4860, 4861..4905, 4906..4950, 4951..4995, 4996..5040, 5041..5085, 5086..5130, 5131..5175, 5176..5220, 5221..5265, 5266..5310, 5311..5355, 5356..5400, 5401..5445, 5446..5490, 5491..5535, 5536..5580, 5581..5625, 5626..5670, 5671..5715, 5716..5760, 5761..5805, 5806..5850, 5851..5895, 5896..5940, 5941..5985, 5986..6030, 6031..6075, 6076..6120, 6121..6165, 6166..6210, 6211..6255, 6256..6300, 6301..6345, 6346..6390, 6391..6435, 6436..6480, 6481..6525, 6526..6570, 6571..6615, 6616..6660, 6661..6705, 6706..6750, 6751..6795, 6796..6840, 6841..6885, 6886..6930, 6931..6975, 6976..7020, 7021..7065, 7066..7110, 7111..7155, 7156..7200, 7201..7245, 7246..7290, 7291..7335, 7336..7380, 7381..7425, 7426..7470, 7471..7515, 7516..7560, 7561..7605, 7606..7650, 7651..7695, 7696..7740, 7741..7785, 7786..7830, 7831..7875, 7876..7920, 7921..7965, 7966..8010, 8011..8055, 8056..8100, 8101..8145, 8146..8190, 8191..8235, 8236..8280, 8281..8325, 8326..8370, 8371..8415, 8416..8460, 8461..8505, 8506..8550, 8551..8595, 8596..8640, 8641..8685, 8686..8730, 8731..8775, 8776..8820, 8821..8865, 8866..8910, 8911..8955
|
| |



