Question 1209608: Find all values of t such that t - 1, t + 1, and 6 - t could be the lengths of the sides of a right triangle.
Found 3 solutions by timofer, josgarithmetic, ikleyn:
Answer by timofer(105)   (Show Source): (Show Source):
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find all values of t such that t - 1, t + 1, and 6 - t could be
the lengths of the sides of a right triangle.
~~~~~~~~~~~~~~~~~~~~
From the problem, it is clear that t-1 is one of legs, since t-1 is
shorter than t+1.
But looking at (t+1) and (6-t), we can not say which of them is longer;
so, we can not determine in advance, which of these two is the hypotenuse.
Therefore, we should consider two cases separately (a) t+1 > 6-t and (b) t+1 < 6-t.
Case (a). t+1 > 6-t.
Then 6-t is the other leg, while t+1 is the hypotenuse.
So, we write the Pythagorean equation and find t from it
(t-1)^2 + (6-t)^2 = (t+1)^2
t^2 - 2t + 1 + 36 - 12t + t^2 = t^2 + 2t + 1
t^2 - 16t + 36 = 0
 = =  = = 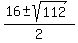 = = 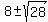 .
So, one root is t = .
So, one root is t = 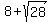 = 13.29 (approx.);
other root is t = = 13.29 (approx.);
other root is t = 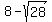 = 2.71 (approx.).
The root t = = 2.71 (approx.).
The root t = 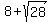 = 13.29 does not work for the problem,
since then 6-t is negative.
The root t = = 13.29 does not work for the problem,
since then 6-t is negative.
The root t = 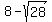 = 2.71 satisfies inequality t+1 > 6 -t.
So, in this case the legs are t-1 = = 2.71 satisfies inequality t+1 > 6 -t.
So, in this case the legs are t-1 =  = 1.71;
and 6-t = = 1.71;
and 6-t =  = 3.29;
the hypotenuse is t+1 = = 3.29;
the hypotenuse is t+1 =  = 3.71.
So, in this case the hypotenuse is really longer than the legs,
and the triangle inequalities are satisfied, which is easy to check.
Thus this case (a) is one possible solution.
Case (b). t+1 < 6-t.
Then 6-t is the hypotenuse, while t+1 is the other leg.
So, we write the Pythagorean equation and find t from it
(t-1)^2 + (t+1)^2 = (6-t)^2
t^2 - 2t + 1 + t^2 + 2t + 1 = 36 - 12t + t^2
t^2 + 12t - 34 = 0 = 3.71.
So, in this case the hypotenuse is really longer than the legs,
and the triangle inequalities are satisfied, which is easy to check.
Thus this case (a) is one possible solution.
Case (b). t+1 < 6-t.
Then 6-t is the hypotenuse, while t+1 is the other leg.
So, we write the Pythagorean equation and find t from it
(t-1)^2 + (t+1)^2 = (6-t)^2
t^2 - 2t + 1 + t^2 + 2t + 1 = 36 - 12t + t^2
t^2 + 12t - 34 = 0
 = =  = = 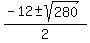 = = 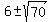 .
So, one root is t = .
So, one root is t = 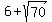 = 14.37 (approx.);
other root is t = = 14.37 (approx.);
other root is t = 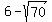 = -2.37 (approx.).
These roots do not work for this problem since t = 14.37 will create negative 6-t,
while t = -2.37 creates both negative t+1 and t-1.
CONCLUSION. In this problem, the only solution is t = = -2.37 (approx.).
These roots do not work for this problem since t = 14.37 will create negative 6-t,
while t = -2.37 creates both negative t+1 and t-1.
CONCLUSION. In this problem, the only solution is t = 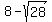 = 2.71;
the legs are t-1 = = 2.71;
the legs are t-1 =  = 1.71 and 6-t = = 1.71 and 6-t =  = 3.29;
the hypotenuse is t+1 = = 3.29;
the hypotenuse is t+1 =  = 3.71. = 3.71.
Solved in full.
-------------------------
The lessons to learn from my post
(a) There are two major cases that should be analyzed separately.
(b) Each case leads to a quadratic equation.
Equations should be solved and their roots should be analyzed for all possible restrictions.
(c) At the end, the triangle inequalities should be checked.
|
|
|