Tutors Answer Your Questions about Pythagorean-theorem (FREE)
Question 552515: please help me to solve the following word problem. A 20 foot ladder is leaned against a wall. If the base of the ladder is 8 feet from the wall, how high up the wall will the ladder reach?
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1209608: Find all values of t such that t - 1, t + 1, and 6 - t could be the lengths of the sides of a right triangle.
Found 3 solutions by ikleyn, josgarithmetic, timofer:
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find all values of t such that t - 1, t + 1, and 6 - t could be
the lengths of the sides of a right triangle.
~~~~~~~~~~~~~~~~~~~~
From the problem, it is clear that t-1 is one of legs, since t-1 is
shorter than t+1.
But looking at (t+1) and (6-t), we can not say which of them is longer;
so, we can not determine in advance, which of these two is the hypotenuse.
Therefore, we should consider two cases separately (a) t+1 > 6-t and (b) t+1 < 6-t.
Case (a). t+1 > 6-t.
Then 6-t is the other leg, while t+1 is the hypotenuse.
So, we write the Pythagorean equation and find t from it
(t-1)^2 + (6-t)^2 = (t+1)^2
t^2 - 2t + 1 + 36 - 12t + t^2 = t^2 + 2t + 1
t^2 - 16t + 36 = 0
 = =  = = 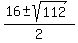 = = 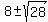 .
So, one root is t = .
So, one root is t = 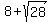 = 13.29 (approx.);
other root is t = = 13.29 (approx.);
other root is t = 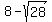 = 2.71 (approx.).
The root t = = 2.71 (approx.).
The root t = 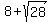 = 13.29 does not work for the problem,
since then 6-t is negative.
The root t = = 13.29 does not work for the problem,
since then 6-t is negative.
The root t = 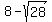 = 2.71 satisfies inequality t+1 > 6 -t.
So, in this case the legs are t-1 = = 2.71 satisfies inequality t+1 > 6 -t.
So, in this case the legs are t-1 =  = 1.71;
and 6-t = = 1.71;
and 6-t =  = 3.29;
the hypotenuse is t+1 = = 3.29;
the hypotenuse is t+1 =  = 3.71.
So, in this case the hypotenuse is really longer than the legs,
and the triangle inequalities are satisfied, which is easy to check.
Thus this case (a) is one possible solution.
Case (b). t+1 < 6-t.
Then 6-t is the hypotenuse, while t+1 is the other leg.
So, we write the Pythagorean equation and find t from it
(t-1)^2 + (t+1)^2 = (6-t)^2
t^2 - 2t + 1 + t^2 + 2t + 1 = 36 - 12t + t^2
t^2 + 12t - 34 = 0 = 3.71.
So, in this case the hypotenuse is really longer than the legs,
and the triangle inequalities are satisfied, which is easy to check.
Thus this case (a) is one possible solution.
Case (b). t+1 < 6-t.
Then 6-t is the hypotenuse, while t+1 is the other leg.
So, we write the Pythagorean equation and find t from it
(t-1)^2 + (t+1)^2 = (6-t)^2
t^2 - 2t + 1 + t^2 + 2t + 1 = 36 - 12t + t^2
t^2 + 12t - 34 = 0
 = =  = = 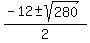 = = 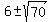 .
So, one root is t = .
So, one root is t = 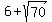 = 14.37 (approx.);
other root is t = = 14.37 (approx.);
other root is t = 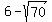 = -2.37 (approx.).
These roots do not work for this problem since t = 14.37 will create negative 6-t,
while t = -2.37 creates both negative t+1 and t-1.
CONCLUSION. In this problem, the only solution is t = = -2.37 (approx.).
These roots do not work for this problem since t = 14.37 will create negative 6-t,
while t = -2.37 creates both negative t+1 and t-1.
CONCLUSION. In this problem, the only solution is t = 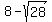 = 2.71;
the legs are t-1 = = 2.71;
the legs are t-1 =  = 1.71 and 6-t = = 1.71 and 6-t =  = 3.29;
the hypotenuse is t+1 = = 3.29;
the hypotenuse is t+1 =  = 3.71. = 3.71.
Solved in full.
-------------------------
The lessons to learn from my post
(a) There are two major cases that should be analyzed separately.
(b) Each case leads to a quadratic equation.
Equations should be solved and their roots should be analyzed for all possible restrictions.
(c) At the end, the triangle inequalities should be checked.
Answer by josgarithmetic(39625)  (Show Source): (Show Source):
Answer by timofer(105)  (Show Source): (Show Source):
Question 1209579: In the diagram, $ABCD$ is a square. Find $PR.$
[asy]
unitsize(1.5 cm);
pair A, B, C, D, P, R;
A = (-1,1);
B = (1,1);
C = (1,-1);
D = (-1,-1);
P = (0,1) + dir(50);
R = -P;
draw(A--B--C--D--cycle);
draw(A--P--B);
draw(C--R--D);
label("$A$", A, W);
label("$B$", B, dir(0));
label("$C$", C, dir(0));
label("$D$", D, W);
label("$P$", P, N);
label("$R$", R, S);
label("$4$", (B + P)/2, NE, red);
label("$8$", (A + P)/2, NW, red);
label("$4 \sqrt{5}$", (A + B)/2, S, red);
label("$4$", (D + R)/2, SW, red);
label("$8$", (C + R)/2, SE, red);
label("$4 \sqrt{5}$", (C + D)/2, N, red);
[/asy]
AB=BC=CD=DA=4sqrt5
PA=CR=8
PB=RD=4
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Hello, I am writing to let you know (in case if you don't know it):
this site/forum is for Math problems.
It is expected that the visitors bring formulations of Math problems in traditional wording form.
If necessary, the wording description can be accompanied by a diagram or a link to a diagram.
But posting computer programs in the language of graphing tools is not what we expect from visitors.
Do you get the meaning of my message?
Question 1208814: Solve for x.
(x + 1)^2 + (x - 1)^2 = 2x
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1208815: Solve for x.
[(1/(2x)]^2 + [(2/(3x)]^2 = 47x
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1208478: A hummingbird's nest is 12 meters high in a tree and a flower is on the ground 5 meters away from the base of the tree. How far will the hummingbird need to fly to get from its nest to the flower?
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The shortest distance between two points is the straight line, connecting the points.
Surely, the hummingbird, being a disciplined rational creature, will choose the straight line to fly.
So, this problem is about a triangle.
You may even make one step forward and to see (or to guess/to recognize) a right-angled triangle here.
As soon as you identify a right angled triangle, apply the Pythagorean formula
d = 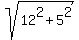 = = 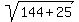 = =  = 13 meters. ANSWER
(5,12,13) is a Pythagorean triple, next after (3,4,5). = 13 meters. ANSWER
(5,12,13) is a Pythagorean triple, next after (3,4,5).
Solved.
Question 1207589: In the diagram, ABCD is a square. Find sin angle PAQ.
P is on BC such that BP = 2 and PC = 3, and Q is on CD such that CQ = 2 and QD = 3.
Found 3 solutions by ikleyn, Edwin McCravy, math_tutor2020:
Answer by ikleyn(52852)   (Show Source): (Show Source):
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
This is possibly what the diagram looks like

Focus on right triangle PAB.
We'll use the tangent trig ratio to determine the following.
tan(angle) = opposite/adjacent
tan(angle PAB) = PB/AB
tan(angle PAB) = 2/5
angle PAB = arctan(2/5)
angle PAB = 21.801409 degrees approximately.
Now move your attention to right triangle DAQ.
tan(angle) = opposite/adjacent
tan(angle DAQ) = DQ/AD
tan(angle DAQ) = 3/5
angle DAQ = arctan(3/5)
angle DAQ = 30.963757 degrees approximately.
Then,
(angleDAQ) + (anglePAQ) + (anglePAB) = angleDAB
(angleDAQ) + (anglePAQ) + (anglePAB) = 90
anglePAQ = 90 - (angleDAQ + anglePAB)
anglePAQ = 90 - (30.963757 + 21.801409)
anglePAQ = 37.234834 degrees approximately
sin(angle PAQ) = sin(37.234834) = 0.605083 approximately
------------------------------------------------------------------------------------
Another approach.
Use the Pythagorean Theorem to determine these lengths
QA = sqrt(5^2+3^2) = 5.830952 approximately
PA = sqrt(5^2+2^2) = 5.385165 approximately
QP = sqrt(2^2+3^2) = 3.605551 approximately
Focus on triangle PAQ of the diagram shown above.
Use the Law of Cosines to find angle PAQ.
a^2 = b^2+c^2-2*b*c*cos(A)
(QP)^2 = (QA)^2+(PA)^2-2*(QA)*(PA)*cos(angle PAQ)
(3.605551)^2 = (5.830952)^2+(5.385165)^2-2*(5.830952)*(5.385165)*cos(angle PAQ)
12.999998 = 63.000003 -62.801277*cos(angle PAQ)
12.999998 - 63.000003 = -62.801277cos(angle PAQ)
-50.000005 = -62.801277cos(angle PAQ)
cos(angle PAQ) = -50.000005/(-62.801277)
cos(angle PAQ) = 0.796162
angle PAQ = 37.234852
There appears to be some slight rounding error going on.
Compare this value to the previous angle PAQ measure found in the section above.
Question 1207466: The regular hexagon ABCDEF has sides of length 2. The point P is the midpoint of AB. Q is the midpoint of BC and so on. Find the area of the hexagon PQRSTU.
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the area of a hexagon is equal to 3 * sqrt(3) / 2 * a^2, where a is the length of one side of the regular hexagon.
the area of your original hexagon is equal to 3 * sqrt(3) / 2 * 2^2 = 10.39230485.
when you connect the midpoints of two adjacent triangles formed by your hexagon, then the side of that new hexagon is equal to 1.732050808.
the area of the new hexagon is equal to 3 * sqrt(3) / 2 * 1.732050808^2 = 7.794228634.
that should be your answer.
the only question you might have is how i derived the value of the side of the new hexagon formed by the midpoints of the original hexagon.
that takes a little explaining.
see my worksheet below.
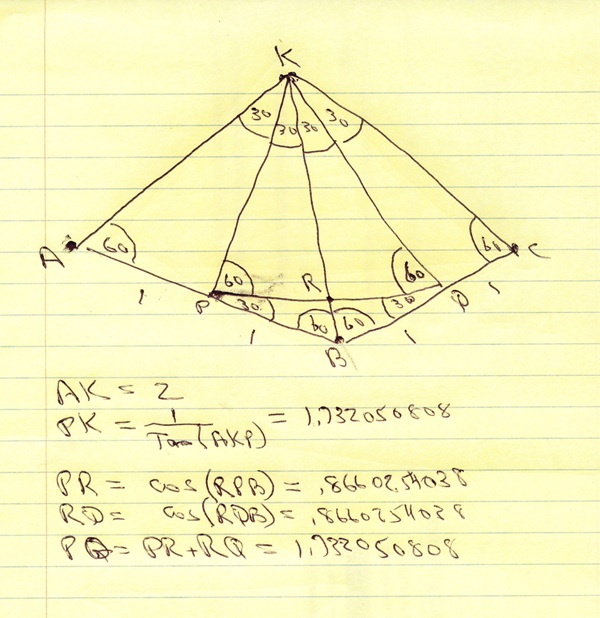
in the diagram:
K is the center of the hexagon.
AKB is one triangle formed from the center of the hexagon to the sides of the hexagon.
BKC is an adjacent triangle formed from the center of the hexagon to the sides of the hexagon.
KP is a line from the center of the hexagon to the midpoint of one side of the hexagon.
KQ is a line from the center of the hexagon to the midpoint of an adjacent side of the hexagon.
the length of AB is 2 and the length of BC is 2.
you form one side of the new hexagon by connecting point P to Q.
that forms triangle PKQ which is one of the 6 triangles of the new hexagon.
angle AKB is split in two by the line KP which terminates at the midpoint of line AB.
AK is the hypotenuse of right triangle AKP.
angle AKP is 30 degrees.
sine(30) = 1 / AK
AK = 1 / sine(30) = 2.
that's how the length of AK was derived to be 2.
PK = 1.732050808.
that's found because tan(30) = 1 / PK
PK = 1 / tan(30) which is equal to 1.732050808.
when you connect point P to Q, that line intersects with line KB at point R.
that forms right triangle PRB.
the hypotenuse of that right triangle is PB whose length is equal to 1.
cosine (RPB) = PR / 1
solve for PR to get PR = 1 * cosine(RPB)
that becomes cosine(30) = .8660254038.
the length of PQ is twice that to be equal to 1.732050808.
that's one side of your new hexagon.
area of your new hexagon is equal to 3 * sqrt(3) / 2 * 1.732050808 = 7.794228634.
that should be your answer.
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1207407: How many right triangles have a hypotenuse that measures 4x + 5 inches and legs that measure 3x + 13 inches and x inches? What are the dimensions of the triangle(s)?
Let me see.
I must use a^2 + b^2 = c^2.
Yes?
My set up:
(3x + 13)^2 + x^2 = (4x + 5)^2
If this is correct, what does the value of x represent in this case?
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
Looks good so far.
(3x + 13)^2 + x^2 = (4x + 5)^2
(3x + 13)(3x + 13) + x^2 = (4x + 5)(4x + 5)
9x^2+39x+39x+169 + x^2 = 16x^2+20x+20x+25
10x^2+78x+169 = 16x^2+40x+25
0 = 16x^2+40x+25-(10x^2+78x+169)
0 = 16x^2+40x+25-10x^2-78x-169
0 = 6x^2-38x-144
6x^2-38x-144 = 0
From here use the quadratic formula.
I'll let the student finish up.
Question 1008558: A farmer's conveyor belt carries hay bales from the ground to the barn loft which is 12 ft from the ground. The conveyor rises at a 60 degree angle. a.)If the bales are moving at a 10 ft/min, how many minutes does it take for them to make it to the loft? b.) how far from the barn does the conveyor belt begin?
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! A farmer's conveyor belt carries hay bales from the ground to the barn loft which is 12 ft from the ground. The conveyor rises at a 60 degree angle. a.)If the bales are moving at a 10 ft/min, how many minutes does it take for them to make it to the loft? b.) how far from the barn does the conveyor belt begin?
Length of belt = 12/sin 60 =13.856 feet
bales move at 10 ft/m
13.856/10 = .1.39 minutes to move to loft
distance of belt from barn = 12/tan 60 =6.93 feet
Question 1206358: A painter leans a 26-foot extension ladder against a building, with the
base 10 feet away from a 24-foot wall. The person using the ladder
feels unsafe and moves the base of the ladder 3 feet closer to the wall.
How much shorter will the ladder need to be to reach the same height
on the wall? Round to the nearest foot, if necessary.
Ⓐ 1 foot
Ⓑ 3 feet
Ⓒ 22 feet
Ⓓ 23 feet
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! A painter leans a 26-foot extension ladder against a building, with the
base 10 feet away from a 24-foot wall. The person using the ladder
feels unsafe and moves the base of the ladder 3 feet closer to the wall.
How much shorter will the ladder need to be to reach the same height
on the wall? Round to the nearest foot, if necessary.
The ladder is shifted 3ft closer to the wall.
The base of ladder now is 7 ft from the wall
The length of ladder = sqrt(24^2+7^2)= 25
So, the ladder will need to be 26−25=1
foot shorter to reach the same height .
 . .
Question 1206302: A ladder is leaning up against a house. If the angle of the ladder with the ground is 58° and the ladder is 20 feet long, how far away from the house is the foot of the ladder?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! let the distance between the foot of the ladder and the foot of the wall of the house be equal to x.
cos(58) = x/20
multiply both sides of this equation by 20 to get x = 20 * cos(58) = 10.598.
your solution is that the distance between the foot of the ladder and the foot of the wall of the house is 10.598 feet.
Question 1206046: Abigail's bedroom is rectangular. The length of one wall of Abigail's bedroom is 6 meters. The length from one corner of the bedroom to the diagonally opposite corner is 7 meters. What is the length of the other wall? If necessary, round to the nearest tenth.
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Question 1205897: Sides of a triangle are 8,11,13.find the largest angle of the triangle
Thank you!
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the largest angle will be opposite the largest side.
if the triangle is ABC, then side a is opposite angle A, side b is opposite angle B, and side c is opposite angle C.
you can use the law of cosines to find angle C.
the law of cosines is c^2 = a^2 + b^2 - 2abcos(C).
that becomes 13^2 = 8^2 + 11^2 - 2*8*11*cos(C).
add 2*8*11*cos(C) to both sides of the and subtract 13^2 from both sides of the equation to get 2*8*11*cos(C) = 8^2 + 11^2 - 13^2.
divide both sides of the equation by (2*8*11) to get cos(C) = (8^2 + 11^2 - 13^2) / (2 * 8 * 11) = .0909091909.
arcos(.0909090909) = 84.78409143 degrees
that's angle C.
you can use the law of sines to find angle B.
that law says sin(C) / c = sin(B) / b.
that becomes sin(84.78409143)/13 = sin(B)/11.
solve for sin(B) to get sin(B) = sin(84.78409143)/13 * 11 = .8426500885.
arcsin(.842650885) = 57.42102961 degrees.
since the sum of the interior angles of a triangle = 180 degrees, then angle A = 180 - 84.78409143 - 57.42102961 = 37.79487896.
the largest angle is opposite the largest side and the smallest angle is opposite the smallest side with the middle angle opposite the middle side.
here are the results in a table of values.
side sine of angle angle
8 .612836428 37.79487896
11 .8426500885 57.42102961
13 .9958591955 84.78409143
sum of the angles is 180 as it should be.
here's my diagram
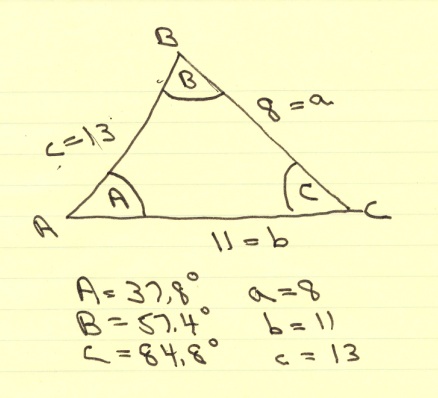
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1205848: Given ABCD is a trapezoid with BC parallel to AD. If AB = AD = 4, angle A = 60 degrees, and angle C = 45 degrees, determine the value of length DC.
Found 3 solutions by math_tutor2020, AnlytcPhil, Edwin McCravy:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
Answer by AnlytcPhil(1807)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The above solution is correct. So that the labeling
ABCD will be counter-clockwise, you can draw the mirror
image of the above solution.
AnlytcPhil aka Edwin
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
Question 1205300: a=12 b=5 c=?
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1205198: jill's front door is 42" wide and 84" tall. she purchased a circular table that is 96 inches in diameter. will the table fit through the front door? Please explain how you found this answer.
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Try if the table will fit to the diagonal of the rectangular door.
For it, compare the diagonal with the diameter of the table.
The diagonal is 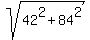 = = 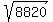 = 93.92 inches (approximately).
Now you respond and explain. = 93.92 inches (approximately).
Now you respond and explain.
Solved, with all necessary explanations.
Question 1204687: Connor's school is due west of his house and due south of his friend Dylan's house. The distance between the school and Dylan's house is 8 kilometers and the straight-line distance between Connor's house and Dylan's house is 10 kilometers. How far is Connor's house from school?
Answer by MathLover1(20850)   (Show Source): (Show Source):
Question 1204612: suppose Q is the midpoint of PR, PQ=x+10, and QR=4x-2.
what is the value of PR?
Answer by josgarithmetic(39625)  (Show Source): (Show Source):
Question 1204257: From a second-storey window directly across the street, the angle of elevation of the top of an office building in Makati is 57° 20' and the angle of depression of the base is 18° 10'. If the buildings are 38 m. apart, what is the height of the building?
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)  (Show Source): (Show Source):
You can put this solution on YOUR website!
57° 20' = 57 + (20/60) = 57.33333° approximately
18° 10' = 18 + (10/60) = 18.16667° approximately
Diagram

The person's eye is located at point A.
B is just across from A.
C and D are the top and base of the other building.
Focus on triangle ABC.
tan(angle) = opposite/adjacent
tan(angle CAB) = BC/AB
tan(57.33333°) = x/38
x = 38*tan(57.33333°)
Now turn your focus to triangle ABD.
tan(angle) = opposite/adjacent
tan(angle DAB) = BD/AB
tan(18.16667°) = y/38
y = 38*tan(18.16667°)
The total height of CD is
CD = CB + BD
CD = x + y
CD = 38*tan(57.33333°) + 38*tan(18.16667°)
CD = 38*( tan(57.33333°) + tan(18.16667°) )
CD = 71.73617
The building is roughly 71.736 meters tall.
Round this approximate value however your teacher instructs.
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The height of the building is 38*tan(57° 20') + 38*tan(18° 10') meters.
You calculate the rest.
If you need explanations, make a sketch and recall the definition of the tangent function.
Solved.
Question 1202538: Ella's computer monitor has a 20-inch screen, which means that the length of the diagonal of the screen is 20 inches. There is a 1-inch margin along the four sides of the screen.
The monitor can be laid flat so that it just fits into a box that is 11 inches wide. How long is the box?
Found 2 solutions by ikleyn, josgarithmetic:
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Ella's computer monitor has a 20-inch screen, which means that the length of the diagonal
of the screen is 20 inches. There is a 1-inch margin along the four sides of the screen.
The monitor can be laid flat so that it just fits into a box that is 11 inches wide.
How long is the box?
~~~~~~~~~~~~~~~~~~~~~~~~
From the problem, we conclude that one of the two dimensions of the screen is
11 - 1 - 1 = 9 inches.
Hence, applying the Pythagoras, we find that the other dimension of the screen is 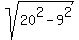 = = 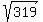 = 17.86 inches (rounded).
It tells us that the corresponding dimension of the box is 17.86 + 1 + 1 = 19.86 inches.
Since this dimension is greater than 11 inches, we have every reason to call this dimension
as "the length of the box".
ANSWER. The length of the box is 19.86 inches. = 17.86 inches (rounded).
It tells us that the corresponding dimension of the box is 17.86 + 1 + 1 = 19.86 inches.
Since this dimension is greater than 11 inches, we have every reason to call this dimension
as "the length of the box".
ANSWER. The length of the box is 19.86 inches.
Solved.
Answer by josgarithmetic(39625)  (Show Source): (Show Source):
You can put this solution on YOUR website! Draw and label the description. Find that this screen is width of  inches. Now you want to find length of the screen, just the screen. Box will be that plus 2 more inches for length. inches. Now you want to find length of the screen, just the screen. Box will be that plus 2 more inches for length.
.
.
Box length 19.8606
Question 1202539: As part of the new year celebrations, the town council decorated the street with banners hung across the tops of buildings. A section of the main street has two buildings 24 meters apart. The heights of the buildings are 13 meters and 20 meters. If the banners are hung tautly, what is the length, in meters, of the shortest banner joining the tops of these Iwo buildings? Write your answer in the space below.
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1202525: A homeowner is to construct a ramp to his frontdoor to make it wheelchair accessible. How long is the ramp if the door is 4ft above and the angle of elevation is 20°?
Answer by josgarithmetic(39625)  (Show Source): (Show Source):
Question 1079272: Mr chen deposit a certain sum of money in a bank in the interest rate of the bank decreases from 3.75% per annum to 3.5% per annum. Mr chen's interest will decrease by $50 in a year. find the sum of money he deposites
Found 2 solutions by greenestamps, mananth:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The other tutor who responded has a habit of supplying answers without checking to see if they are correct. A simple arithmetic error in her response leads to an incorrect answer.
The interest rate decreased by 1/4 of 1 percent, resulting in a decrease of $50 in interest.
A decrease of 1/4 of 1 percent resulting in a decrease of $50 in interest means that a decrease of 1 percent would result in a decrease of 4($50) = $200; that means the amount invested was 100($200) = $20,000.
ANSWER: $20,000
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website! Mr chen deposit a certain sum of money in a bank in the interest rate of the bank decreases from 3.75% per annum to 3.5% per annum. Mr chen's interest will decrease by $50 in a year. find the sum of money he deposites
Mr chen deposit a certain sum of money in a bank let it be x
interest
At 3.75% rate he gets 3.75%x
At 3.50% rate he gets 3.50%x
3.75%x-3.50%x =50
0.0375x-0.0350x =50
0.025x=50
x=50/0.025
x=2000
sum of money in a bank deposited = $2000
Question 1114725: Find the length of the missing side of this figure. Leave your response to that command in the simplest radical form your response to that command can be.
There is an image involved in that command.
Go to here to see that image: https://www.connexus.com/content/media/226250-732012-93646-AM-1889155643.png
If you go to Connexus, it will tell you that you must log in to view content that is there.
Log in to Connexus using ZacharyBarringer1 as a username and Zachary98 as a password.
A) 25
B) 144
C) 5
D) Square root 5
Answer by mananth(16946)   (Show Source): (Show Source):
Question 1202038: A kite is flying 10-ft off the ground. Its line is pulled taut and casts a 6-ft shadow. Find the length of the line. If necessary, round your answer to the nearest tenth.
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1202037: A kite is flying 10-ft off the ground. Its line is pulled taut and casts a 6-ft shadow. Find the length of the line. If necessary, round your answer to the nearest tenth.
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1201913: A 16 -inch laptop has a screen that is 7 inches tall. How wide is the screen?
Found 2 solutions by Alan3354, mananth:
Answer by Alan3354(69443)   (Show Source): (Show Source):
You can put this solution on YOUR website! A 16 -inch laptop has a screen that is 7 inches tall. How wide is the screen?
----------
If the diagonal is 16 inches:
w^2 + 7^2 = 16^2
Answer by mananth(16946)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A 16 -inch laptop has a screen that is 7 inches tall
diagonal of the rectangular TV =16 "
Height = 7 "
width (w) = ?
We apply Pythagoras theorem
w^2+h^2= 16^2
w^2 = 16^2-(7^2)
w^2= 207
w = sqrt(207)
Simplify
Question 1201807: what is the length in simplified form, of the hypotenuse of a right triangle whose legs are 27 and 31 units long?
Answer by ikleyn(52852)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Apply the Pythagorean formula
the hypotenuse length = 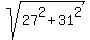 = use your calculator = 41.10961 (rounded). ANSWER = use your calculator = 41.10961 (rounded). ANSWER
Is it so difficult to answer ?
Question 1201282: A right triangle’s hypotenuse is 6 cm, and one leg is
√5 cm. Find the length of the other leg.
Answer by josgarithmetic(39625)  (Show Source): (Show Source):
Question 1200949: Luna takes a sheet of paper and makes a diagonal cut from one corner to the opposite corner, making two triangles. The cut she makes is 10 inches long and the width of the paper is 9 inches. What is the paper's length? If necessary, round to the nearest tenth.
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1200951: From her home, Ling would have to walk due north to get to her friend Allie's house and due east to get to her friend Reid's house. It is 5 miles from Ling's house to Reid's house and a straight-line distance of 7 miles from Allie's house to Reid's house. How far is Ling's house from Allie's house? If necessary, round to the nearest tenth.
Answer by ikleyn(52852)   (Show Source): (Show Source):
Question 1200948: Mandy is mountain climbing with Erin and has just climbed an 18-meter vertical rock face. Erin is standing at the bottom of the cliff, looking up at Mandy. If Erin is 30 meters away from Mandy, how far away from the cliff is Erin standing?
Answer by ikleyn(52852)   (Show Source): (Show Source):
|
Older solutions: 1..45, 46..90, 91..135, 136..180, 181..225, 226..270, 271..315, 316..360, 361..405, 406..450, 451..495, 496..540, 541..585, 586..630, 631..675, 676..720, 721..765, 766..810, 811..855, 856..900, 901..945, 946..990, 991..1035, 1036..1080, 1081..1125, 1126..1170, 1171..1215, 1216..1260, 1261..1305, 1306..1350, 1351..1395, 1396..1440, 1441..1485, 1486..1530, 1531..1575, 1576..1620, 1621..1665, 1666..1710, 1711..1755, 1756..1800, 1801..1845, 1846..1890, 1891..1935, 1936..1980, 1981..2025, 2026..2070, 2071..2115, 2116..2160, 2161..2205, 2206..2250, 2251..2295, 2296..2340, 2341..2385, 2386..2430, 2431..2475, 2476..2520, 2521..2565, 2566..2610, 2611..2655, 2656..2700, 2701..2745, 2746..2790, 2791..2835, 2836..2880, 2881..2925, 2926..2970, 2971..3015, 3016..3060, 3061..3105, 3106..3150, 3151..3195, 3196..3240, 3241..3285, 3286..3330, 3331..3375, 3376..3420
|




 .
.


 .
.