SOLUTION: In a 100 page book, pages 2 and 3 face each other. Similarly, pages 4 and 5 and 6 and 7 face each other. This pattern is repeated to the end of the book. The sum of two facing page

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: In a 100 page book, pages 2 and 3 face each other. Similarly, pages 4 and 5 and 6 and 7 face each other. This pattern is repeated to the end of the book. The sum of two facing page      Log On


   

Question 831743: In a 100 page book, pages 2 and 3 face each other. Similarly, pages 4 and 5 and 6 and 7 face each other. This pattern is repeated to the end of the book. The sum of two facing pages could be-
1. 97
2. 99
3. 90
4. 95
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The page facing the front of the book is always an odd-numbered page (1, 3, 5, and so on).
On the back of that page is an even numbered page (2, 4, 6, and so on) and that even page is facing the next numbered (odd-numbered) page.
As you open the book to see two pages that are facing each other,
the page on the left will have an even number x ,
and the one on the right will have number x%2B1 .
When you add the numbers you get
SUM=x%2Bx%2B1=2x%2B1 .
That sum is an odd number, but if you solve for x :
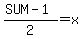
SUM=2x%2B1--->SUM-1=2x---> %28SUM-1%29%2F2=x
x must be an even number.
highlight%28SUM=97%29 works, because x=%2897-1%29%2F2=96%2F2=48 and 48 is an even number.
SUM=99 does not work, because you get an odd number for x : x=%2899-1%29%2F2=98%2F2=49 .
SUM=95 does not work because it gives you an odd x again.
We do not even try SUM=90 because we know that the sum must be odd, and 90 is even.

NOTE:
This is the kind of problem that you could encounter in a test like the SAT, where you have to think fast through too many questions. Depending on the scoring procedure, if you can eliminate one choice, guessing could help.
For this question, you should be able to eliminate 90 right away.