Questions on Word Problems: Problems with consecutive odd even integers answered by real tutors!

Tutors Answer Your Questions about Problems-with-consecutive-odd-even-integers (FREE)

Question 1208747: Find two consecutive positive integers such that the square of the first
increased by 2 times the second is equal to 37.

Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!

There are multiple ways to interpret the wording of this problem. Ikleyn picked a way that did have a solution in positive integers, the first way below. However, the others are also valid ways to interpret the problem, although some of the others likely do not have positive integer solutions. Algebra problem-creators should be more careful to avoid ambiguous sentences. 1. Find two consecutive positive integers such that (the square of the first) increased by (2 times the second) is equal to 37. 2. Find two consecutive positive integers such that [(the square of the first) increased by 2] times the second is equal to 37. 3. Find two consecutive positive integers such that [the square of (the first increased by 2)] times the second is equal to 37. 4. Find two consecutive positive integers such that the square of [(the first increased by 2) times the second] is equal to 37. 5. Find two consecutive positive integers such that the square of [the first increased by (2 times the second)] is equal to 37. 6. Find two consecutive positive integers such that [the square of (the first increased by 2) times the second] is equal to 37. Edwin

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Find two consecutive positive integers such that the square of the first
increased by 2 times the second is equal to 37.
~~~~~~~~~~~~~~~~~~~~~

Let first (smaller) positive integer be n; then the next consecutive integer number is (n+1). Write an equation according to the problem n^2 + 2*(n+1) = 37. Simplify n^2 + 2n + 2 = 37, n^2 + 2n - 35 = 0 Factorize (n+7)*(n-5) = 0. The roots are n= -7 and n= 5. We want the positive value. ANSWER. The numbers are 5 and 6. CHECK. 5^2 + 2*6 = 25 + 12 = 37. ! correct !

Solved.

/////////////////////////

Based on Edwin's note, someone can write a Master thesis or even a PhD dissertation in Math education :).

As an epigraph to such a Master thesis or PhD dissertation the person may write
that word problems in English often require a small auxiliary volume of explanations
of used terms and of what exactly means by the author, and what does not mean.

Question 1207267: 4. Two numbers differ by 9 and the sum of their reciprocals is 5/12. Find the numbers.
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

1st Hint:
One setup equation would be

2nd hint:
Multiply both sides by the LCD 12x(x+9) to arrive at

3rd hint:
Expand everything out and get terms to one side.
You should get
In which you can use the quadratic formula.

Question 634306: Given three consecutive odd numbers such that the square of the second number is 192 less than the square of the third. Find those numbers.
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
consecutive ODD numbers
2n-1, 2n+1, 2n+3

The odd numbers are 45, 47, 49

Question 1206045: A number is such that thrice the number is 14 what is then 5 times number find the number

Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!

If 3n = 14, what is 5n? Do you want to know 5n or n or both? Solve the equation and if you want n, you'll have it. If you want 5n, multiply by 5. Edwin

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
A number is such that thrice the number is 14 what is then 5 times number find the number
~~~~~~~~~~~~~~~~~~~~~

                        Isn't it obvious ?

Question 1205039: A popular band wants to sell $9,099 worth of tickets on its upcoming tour. If each ticket costs $2, how many tickets will the band have to sell to meet its goal?

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

Divide 9,099 dollars by 2; then take the closest integer from the top for the number of tickets. ANSWER. 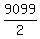---> 4549.5 ---> 4550 tickets.

Solved.

The level of difficulty is as 5 divide by 2.

------------------------

Posting such tasks to the forum can only be done out of idleness.

Question 1205024: In a right angle triangle ABC side AC is 4cm shorter than the hypotenuse and side BC is also 4cm shorter than the hypotenuse. Find the dimensions of the triangle
Found 2 solutions by mananth, ikleyn:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!

In a right angle triangle ABC side AC is 4cm shorter than the hypotenuse and side BC is also 4cm shorter than the hypotenuse. Find the dimensions of the triangle
Since it is a right angled triangle we apply pythagoras theorem
let hypotenuse be x
AC= x-4
BC = x-4
(x-4)^2+(x-4)^2= x^2
2(x-4)^2=x^2
2(x^2-8x+16)=x^2
2x^2-16x+32=x^2
subtract x^2 from both sides
x^2-16x+32=0
add 64 to both sides to solve by comp;eting the square metod
(x^2-16x+64)+32=64
(x-8)^2= 64-32
(x-8)^2= 32
take square root
x-8= +/- sqrt(32)
x= 8+/-sqrt(32) The hypotenuse
sides are 4 less than the hypotenuse

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
In a right angle triangle ABC side AC is 4cm shorter than the hypotenuse and side BC
is also 4cm shorter than the hypotenuse. Find the dimensions of the triangle
~~~~~~~~~~~~~~~~~~~~~~

x^2 + x^2 = (x+4)^2 <<<---=== Pythagorea equation; x is the common length of any of the two its legs. 2x^2 = x^2 + 8x + 16 x^2 - 8x - 16 = 0 x = = = = . Only positive root is the solution to the problem. ANSWER. The triangle is isosceles right angled triangle. Its legs are cm long. Its hypotenuse is = cm long.

Solved.

--------------------

Warning to a reader

        The solution by @mananth, giving two possible solutions for the hypotenuse, is NOT precisely correct.

        Only one (greater) of the two values of the hypotenuse length is admittable;
        the second (lesser) value is NOT admittable, since it leads to negative value of the leg length.

Question 1205018: There are three consecutive odd integers. The sum of quadruple the largest and twice the smallest is 46. What is the middle integer?
Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!

let’s three odd consecutive integers be , , and
if the sum of quadruple the largest and twice the smallest is , we have
...simplify, both sides divide by

integers are: ,,

check

Question 1204967: Tony found four consecutive even integers such that 5 times the sum of the first and third was 9604 greater than twice the sum of the second and the fourth. Find the numbers and express each in standard form.
Found 2 solutions by mananth, math_tutor2020:
Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!
Tony found four consecutive even integers such that 5 times the sum of the first and third was 9604 greater than twice the sum of the second and the fourth. Find the numbers and express each in standard form.

n-3, n-1,n+1,n+3

5 times the sum of the first and third was 9604 greater than twice the sum of the second and the fourth.
5(n-3+n+1)= 2(n-1+n+3)+9604
5(2n-2)=2(2n+2)+9604
10n-10 = 4n+4+9604
6n = 9618
n= 1603
n-3= 1603-3= 1600
n-1= 1603-1= 1602
n+11603+1=1604
n+3= 1603+3- 1606
CHECK
5*(1600+1604)= 2(1602+1606)+9604 =16020

Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

1st number = x = some even integer
2nd number = x+2 = the even integer just after x
3rd number = x+4 = the even integer just after x+2
4th number = x+6 = the even integer just after x+4

One possible equation to form is
5(x + x+4) = 2(x+2 + x+6) + 9604
Pay attention to the color coding to see where all the expressions fit in.

The left side is of the form 5*(1st + 3rd)
The right side is of the form 2*(2nd + 4th) + 9604

I'll let the student solve that equation for x.

Question 1204922: A positive integer is 5 less than another. If the reciprocal of the smaller
integer is subtracted from 3 times the reciprocal of the larger,
, then the
result is 1/12. Find the two integers
Found 2 solutions by Theo, josgarithmetic:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website!
let x equal the larger number
let y equal the smaller number

your equation is 3/x - 1/y = 1/12

that equation states that 3 times the reciprocal of the larger number minus the reciprocal of the smaller number is equal to 1/12.

another way of saying that is that the reciprocal of the smaller number is subtracted from 3 time the reciprocal of the larger number.

you start with 3/x - 1/y = 1/12

multiply both sides of the equation by xy to get:

3y - x = xy/12

multiply both sides of the equation by 12 to get:

12 * (3y - x) = xy

simplify to get:

36y - 12x = xy

you are given that y = x-5, so replace y with x-5 in the equation to get:

36 * (x-5) - 12x = x * (x-5)

simplify to get:

36x - 180 - 12x = x^2 - 5x

combine like terms to get:

24x - 180 = x^2 - 5x

subtract 24x from both sides of the equation and add 180 to both sides of the equation to get:

0 = x^2 - 29x + 180

factor this quadratic equation to get:

(x - 20) * (x - 9) = 0

solve for x to get:

x = 20 or x = 9

when x = 20, y = 15
when x = 9, y = 4

your initial equation was 3/x - 1/y = 1/12

when x = 20 and y = 15, the equation becomes 3/20 - 1/15 = 1/12
multiply both sides of this equation by 300 to get 45 - 20 = 25
this results in 25 = 25, confirming the equation is true.

when x = 9 and y = 4, the equation becomes 3/9 - 1/4 = 1/12
multiply both sides of this equation by 36 to get 12 - 9 = 36/12
this results in 3 = 3, confirming the equation is true.

your value pairs of x = 20 and y = 15 or x = 9 and y = 4 both satisfy the requirements of the problem.

you actually have two answers.

the first answer is your integers are 20 and 15.

the second answer is your integers are 9 and 4.

Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
The two integers can start as n and n-5. Notice .

multiply both sides by 12n(n-5), simplify and solve.

-removed-

Question 1204912: find five consecutive integers such that triple the third is equal to 44 more than half the fifth
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
using n for the the number-three positioned integer,

If that makes sense then the rest is simple arithmetic.

16, 17, 18, 19, 20

Question 1204829: The sum of three consecutive integers is 48. Find the integers

Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!

The sum of three consecutive integers is 48. Find the integers
n, n+1, n+2 be the integers
n+n+1+n+2=48
3n+3=48
3n = 48-3
3n=45
n= 15
n+1=16
n+2=17
15,16,17 are the integers

Question 1204742: What is the equation for the following word problem?

The sum of 3 consecutive even integers is no more that 39. What are the two integers?
Found 4 solutions by josgarithmetic, ikleyn, Alan3354, ankor@dixie-net.com:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
Decide which is it! Three integers or two integers. Must be exclusively one or the other of them.

Two integers, consecutive even?
Let them be n and n+2.

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

There are at least TWO fatal errors in your post.

One error is when you are asking about "the two integers".

Article "the" is used when an item after "the" is just defined previously as a subject of discussion.
But in your post, the two numbers are not defined as a subject of discussion - only THREE numbers are defined, but not two of them.

Second error is that you ask about an equation.
Where is NO such equation, at all.
There is only an inequality relevant to this context.

So, it is not surprising that tutors can not answer your question as it is posed.

It is because everything is incorrect there.

The inequality you are asking about is

        (n-2) + n + (n+2) <= 39,

or

        3n <= 39,

where n is the middle of the three consecutive even integers.

After reading your post, it becomes clear, that this "problem" is created/composed/worded/printed
by a person, who does not know neither English nor Math.

///////////////////

There is third fatal error, too.

The number of solutions of this inequality is infinite.
In other words, the number of such triples of integer numbers is infinite.

Therefore, when you ask "what are the two numbers", the question becomes totally undefined.

.............................

Do not even try to create your own Math problems.

To do it properly, 15 year of intensive studying Math is required,
in the school and in the University, PLUS 5-10 years practicing after that.

Tens of textbooks on the subject should be read and thousands problems should be
solved before you become a Math problems composer and writer (if you are lucky).

Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
What is the equation for the following word problem?

The sum of 3 consecutive even integers is no more that 39. What are the two integers?
================
Poorly worded question.
Is it 3 integers or 2?
---

--> n = 12
10 + 12 + 14 = 36

Answer by ankor@dixie-net.com(22740)   (Show Source):
You can put this solution on YOUR website!
The sum of 3 consecutive even integers is no more that 39
The sum of consecutive even integers cannot equal an odd number!!

Question 1204660: There are a total of 20 lions, tigers, and bears at the local zoo. The number of tigers is 2 more than the number of lions. The number of bears is 3 more than the number of lions. How many lions are at the zoo?
Found 4 solutions by math_tutor2020, josgarithmetic, ikleyn, mananth:
Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

Let's make a guess that there are 6 lions because 20/3 = 6.67 approximately. I rounded down to the nearest whole number.

6 lions --> 6+2 = 8 tigers and 6+3 = 9 bears
6 lions + 8 tigers + 9 bears = 23 total animals

We have 3 too many animals. Let's take away 1 of each
6-1 = 5 lions
8-1 = 7 tigers
9-1 = 8 bears
Then,
5 lions + 7 tigers + 8 bears = 20 total animals
We have found the answer.

This method is probably not as efficient as the standard algebraic approach, but it's good to have multiple pathways to any math problem.

Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!

Animals: How Many LIONS L TIGERS L+2 BEARS L+3 Total 20

You see, ?

Then .

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

Even if you are 2-nd grade student and do not know equations yet,
you can easy solve this problem using only your common sense and skills calculating whole numbers.

From 20 animals, take out 2 tigers and 3 bears, for a minute (mentally in your mind).

You will get 15 animals, lions, tigers and bears in equal amount.

What you will do next ? - But of course, you will distribute 15 animal in 3 equal groups.

In other words, you will divide 15 by 3 and will get 5 animals in each group.

After that, you will return back 2 tigers and 3 bears and will get the final answer this way.

----------------

Nice problem for 2-nd grade 7-years old/(young) students.

Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!
There are a total of 20 lions, tigers, and bears at the local zoo.
The number of tigers is 2 more than the number of lions.
Let number of lions be x
Number of tigers will be x+2

The number of bears is 3 more than the number of lions.
The number of bears= x+3
Add them up. They equal 20
x+x+2+x+3=20
3x+5 =20
subtract 5 from both sides
3x+5-5= 20-5
3x=15
divide by 3
x=5
There are 5 lions at the zoo.

Question 1204547: The sum of the reciprocals of two consecutive even integers is 23/264
. Find the two integers.
Found 3 solutions by ikleyn, Alan3354, math_tutor2020:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

I will use an idea, which is close to Alan' solution, but is slightly different. If the sum of the reciprocals of two consecutive even integers is 23/264, then each reciprocal is close to = . Hence, each of the two consecutive even integer is close to = 22.96. From it, I conclude that the two consecutive even integer numbers are 22 and 24. Now it is a matter of arithmetic to check that it is true.

Solved.

Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
The sum of the reciprocals of two consecutive even integers is 23/264
. Find the two integers.
-------------
23/264 = 46/528
--- close to 23
---> 22 & 24

Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

x = first even integer
x+2 = second even integer just after x.

Their reciprocals add to 23/264.

Use the quadratic formula from here.
a = 23, b = -482, c = -528

or

or

or

or
Ignore the non-integer result.

Therefore,

Answer: The two consecutive even integers are 22 and 24.

Question 1204524: Three times the lesser of two consecutive even integers is 6 less than six times the greater number. Find the integers.

Found 3 solutions by josgarithmetic, Alan3354, mananth:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
n, any integer even or odd
2n, an EVEN integer

The two expected integers, 2n and 2n+2

-

RESULT:
Lesser integer, -2
Greater integer, 0

The same result happens if starting with just n and assuming it to be even.

Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website!
Three times the lesser of two consecutive even integers is 6 less than six times the greater number. Find the integers.
---------------
3n + 6 = 6(n+2) = 6n + 12
3n + 6 = 0
n = -2
---> -2 and zero

Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!
Three times the lesser of two consecutive even integers is 6 less than six times the greater number. Find the integers.
let the integers be x and x+2
Three times the lesser of two consecutive even integers is 6 less than six times the greater number.
as per the condition
3x = 6(x+2) -6
3x =6x+12-6
3x= 6x-6
3x-6x = 6x+6-6x
-3x=6
x=-2
x+2=0
-2 , 0 are the integers

Question 1204189: The product of the first and third of three negative consecutive integers is 59 more than 4 times the second integer. Find the integers.

Found 3 solutions by Edwin McCravy, mananth, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!

Let the middle integer be x, then the first one is x-1 and the third one is x+1. x-1 = smallest x = middle x+1 = largest The product of the first and third of three negative consecutive integers That's (x-1)(x+1) is 59 more than 4 times the second integer. Find the integers. That's 4x + 59 (x-1)(x+1) = 4x + 59 x2 - 1 = 4x + 59 x2 - 4x - 60 = 0 (x + 6)(x - 10) = 0 x + 6 = 0; x - 10 = 0 x = -6; x = 10 We are told that the integers are negative, so we discard x=10 x-1 = smallest = -6-1 = -7 x = middle = -6 x+1 = largest = -6+1 = -5 Checking the words: The product of the first and third... (-7)(-5) = 35 ...is 59 more than 4 times the second integer. That's 59 more than 4 times -6, which is -24. Sure enough,' it's true that (-24) + 59 = 35. Edwin

Answer by mananth(16946)   (Show Source):
You can put this solution on YOUR website!
The product of the first and third of three negative consecutive integers is 59 more than 4 times the second integer. Find the integers.
Let the integers be x-1 , x , x+1
(x-1)(x+1)=59+4x
x^2-1-4x =59
x^2-4x-60=0
x^2-10x +6x-60=0
x(x-10)+6(x-10)=0
(x-10)(x+6)=0
x=-6 or 10
the numbers are negative
so x=-6
the integers are -7,-6,-5 as per given condition
CHECK
(x-1)(x+1)=59+4x
(-7)(-5) = 59 -4*(-6)
35 = 35

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.

The integers are (n-1), n, (n+1), and (n-1)*(n+1) = 4n + 59, or n^2 - 1 = 4n + 59, which implies n^2 - 4n - 60 = 0, (n-10)*(n+6) = 0. So, the middle integer can be either 10 or -6. And since the integers are negative, the only possibility is that the three numbers are -7, -6, -5. This and only this triple satisfies the problem's condition.

Solved.

Question 1203894: The sum of three consecutive odd integers is -3. Find the value of the least of the three.
Found 2 solutions by mccravyedwin, greenestamps:
Answer by mccravyedwin(407)   (Show Source):
You can put this solution on YOUR website!

Let x = the value of the least of the three consecutive integers, then x+1 = the value of the middle of the three consecutive integers. And x+2 = the value of the largest of the three consecutive integers. x + x+1 + x+2 = -3. Solve for x. That'll be the answer. Edwin

Answer by greenestamps(13200)   (Show Source):
You can put this solution on YOUR website!

The average of three consecutive odd integers is the middle integer.

In this problem the sum of the three integers is -3, so the average is -3/3 = -1.

So the consecutive odd integers are -3, -1, and 1.

ANSWER: -3

Question 1203880: Find three consecutive integers whose sum is 22 less than two times the larger number

Found 2 solutions by josgarithmetic, MathLover1:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!

-

ANSWER:

Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!

three consecutive integers :
,,
whose sum is less than two times the larger number

=> first integer

three consecutive integers:

,,

Question 1203707: Find five consecutive integers such that:
“The sum of the first and 4 times the third is equal to 56 less than 3 times the sum of the second, fourth, and fifth.”

Found 3 solutions by ikleyn, MathLover1, josgarithmetic:
Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Find five consecutive integers such that:
“The sum of the first and 4 times the third is equal to 56 less than 3 times
the sum of the second, fourth, and fifth.”
~~~~~~~~~~~~~~~~

Let the numbers n, (n+1), (n+2), (n+3) and (n+4) be five consecutive integer numbers. Write equation as you read the problem n + 4*(n+2) = 3*((n+1) + (n+3) + (n+4)) - 56. Simplify step by step n + 4n + 8 = 3*(3n+8) - 56 5n + 8 = 9n + 24 - 56 8 - 24 + 56 = 9n - 5n 40 = 4n n = 40/4 = 10. ANSWER. The numbers are 10, 11, 12, 13, 14.

Solved.

Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!

The formula for a sequence of consecutive integers is , , ,, ,..., .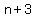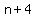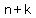
The sum of the first and times the third is equal to less than 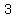times the sum of the second, fourth, and fifth.

five consecutive integers are:, , , ,
check:

Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
Mostly you write the worded description as symbolism literally.

Not the only way to assign, but:
n-2
n-1
n
n+1
n+2

Solve this....

---------------the integer in the middle

**************************this is wrong******************************

-----------NO. This does not check.
MISTAKE SOMEWHERE....

Question 1202926: Find two consecutive odd integers such that 50 more than the lesser is five times the greater.
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20055)   (Show Source):
You can put this solution on YOUR website!

Change 'even' to 'odd' and you can do it. Find two consecutive EVEN integers such that 50 more than the lesser is five times the greater. G = L+2 L+50 = 5G L+50 = 5(L+2) L+50 = 5L+10 40 = 4L 10 = L G = L+2 G = 10+2 G = 12 10 and 12. Or switch "greater" and "lesser" and you can do it. Find two consecutive odd integers such that 50 more than the GREATER is five times the LESSER. G = L+2 G+50 = 5L L+2+50 = 5L L+52 = 5L 52 = 4L 13 = L G = L+2 G = 13+2 G = 15. 13 and 15. There is no solution as you have written it. Maybe your teacher was testing you to see if you'd know it has no solution. Sometimes the correct answer is "no solution". Edwin

Answer by ikleyn(52781)   (Show Source):
You can put this solution on YOUR website!
.
Find two consecutive odd integers such that 50 more than the lesser
is five times the greater.
~~~~~~~~~~~~~~~~~~~~~~~~

Let the numbers be x and (x+2). Then we can write this equation x + 50 = 5*(x+2). Simplify and find x x + 50 = 5x + 10 50 - 10 = 5x - x 40 = 4x x = 40/4 = 10. It shows that the problem is posed INCORRECTLY. Such odd integers as described in your post DO NOT EXIST, and the problem describes a situation which never may happen.

Solved.

======================

It is a grave sin to spread wrong tasks in the Internet.

Question 1202523: The sum of two consecutive even numbers is -382. Find the numbers.
The two consecutive integers from small to large are
_______,__________
.

Found 2 solutions by josgarithmetic, math_tutor2020:
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
Just two even numbers, consecutive?

;

-192 and -190

Answer by math_tutor2020(3817)   (Show Source):
You can put this solution on YOUR website!

x = first even number
x+2 = second even number, adjacent to, and to the right of x.

x+(x+2) = 2x+2 = sum of those values
2x+2 = -382
2(x+1) = -382
x+1 = -382/2
x+1 = -191
x = -191-1
x = -192

Or
2x+2 = -382
2x = -382-2
2x = -384
x = -384/2
x = -192

If x = -192, then x+2 = -192+2 = -190
Check:
(-192)+(-190) = -382

Answer: -192 and -190

Question 1202493: Find three consecutive odd integers such that -3 times the sum of the first and third is 50 greater than 8 times the opposite of the second.
Answer by josgarithmetic(39617)   (Show Source):
You can put this solution on YOUR website!
consecutive odd
n, n+2, n+4

description

simple algebra from here.

.
.
23, 25, 27