Question 951792: A box contains tags marked 1, 2, ... n. Two tags are chosen at random. Find the probability that the numbers on the tags will be consecutive integers if a) the tags are chosen without replacement, and b) the tags are chosen with replacement.
Answer by mathmate(429)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Given:
n tags in a box numbered sequentially from 1 to n. (Assuming n>1)
Two tags are drawn randomly.
Find
(a) probability that the two tags are consecutive, if drawn without replacement
(b) same as (a), but with replacement.
Solution:
Let events
E - first tag is an end tag (1 or n)
I - first tag is not an end tag (interior tags)
C - second tag is consecutive to the first (either way)
For the first tag,
P(E)=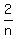 (tags 1 and n out of n tags) (tags 1 and n out of n tags)
P(I) = 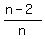 (the non-end tags, or interior tags) (the non-end tags, or interior tags)
(a) without replacement
For the second tag, there are n-1 tags left.
If an end tag was chosen, there is only 1 possible consecutive tag.
If an interior tag was chosen, there are two possible consecutive tags, one higher and one lower than the first tag.
So the probability of drawing two consecutive tags would be
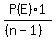 if the first tag is an end tag, and if the first tag is an end tag, and
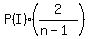 if the first tag is an interior tag. if the first tag is an interior tag.
So probability of two consecutive tags is
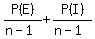
=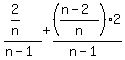
=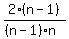
=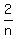
(b) with replacement
When the first tag is mixed into the box, the number of successes does not increase, since identical tags drawn are not consecutive.
Therefore, the probability is decreased by dilution, and can be found by substituting n for n-1 in the denominators.
Probability of consecutive tags with replacement is
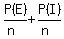
=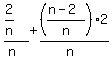
=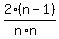
=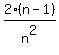
Answer:
(a) probability of picking 2 consecutive numbers = 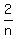 (without replacement) (without replacement)
(b) probability of picking 2 consecutive numbers = 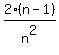 (with replacement) (with replacement)
|
|
|